|
旋转变换<-->旋转变换中图形的变化
线性变换
一般地,如果变换T: 前后坐标之间的关系具有如下关系: 前后坐标之间的关系具有如下关系: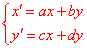 ,也就是 ,也就是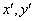 都是x,y的常数项为0的一次函数,就将这样的变换T称为线性变换,此时可以将表达式写成 都是x,y的常数项为0的一次函数,就将这样的变换T称为线性变换,此时可以将表达式写成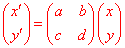 的形式,不同的线性变换的差别仅仅在于一次函数表达式中的4个系数a,b,c,d的不同。因此,这4个数排列成的2行2列的数表 的形式,不同的线性变换的差别仅仅在于一次函数表达式中的4个系数a,b,c,d的不同。因此,这4个数排列成的2行2列的数表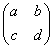 决定了平面上的线性变换。我们将这样由4个数排成的2行2列的数表称为2行2列的矩阵,也称为2×2矩阵,表达式所描述的变化完全由矩阵 决定了平面上的线性变换。我们将这样由4个数排成的2行2列的数表称为2行2列的矩阵,也称为2×2矩阵,表达式所描述的变化完全由矩阵 决定,我们称它为这个变换的矩阵,而称这个变换是由这个矩阵表示的变换。 决定,我们称它为这个变换的矩阵,而称这个变换是由这个矩阵表示的变换。
|

