|
空间向量数量积运算<-->空间向量基本定理
空间向量数量积运算的应用
⑴求证垂直:求证两直线垂直转化为求证两直线的方向向量垂直。
若设两直线的方向向量分别为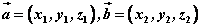 ,则 ,则
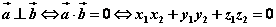
⑵求向量的模:若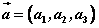 ,则 ,则
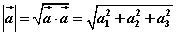 。 。
⑶求两直线的夹角:求两直线的夹角转化为求两直线的方向向量的夹角。
若设两直线的方向向量分别为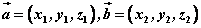 ,则 ,则
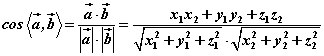 。 。
⑷求两点间的距离:求两点间的距离转化为求以这两点为始终点的有向线段的长度,即求向量的模。
若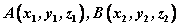 ,则 ,则
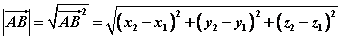 。 。
⑸求平面的法向量:
1o 平面的法向量:如果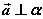 ,那么向量 ,那么向量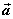 叫做平面 叫做平面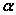 的法向量。 的法向量。
2o 求平面的法向量:
设非零向量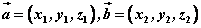 ,使得 ,使得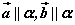 , ,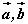 不共线,若非零向量 不共线,若非零向量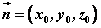 为平面 为平面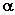 的法向量,则 的法向量,则
 。 。
解得 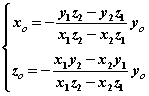 , ,
令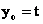 ( (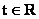 , ,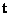 可取使 可取使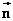 尽量简单的常数值),则法向量 尽量简单的常数值),则法向量
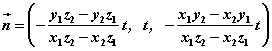 。 。
⑹求空间点面距离:
如图,设平面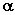 的法向量 的法向量 及平面 及平面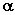 上一点A,则点P到 上一点A,则点P到
平面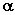 的距离d为 的距离d为
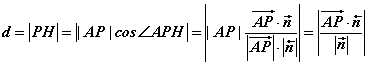 。 。
用向量方法求点面距离的特点是不要作垂线,不要求找到垂足就可以求得点面距离。
⑺求线面所成的角:
设直线L的方向向量为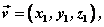 平面 平面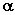 的法向量为 的法向量为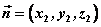 ,向量 ,向量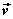 与 与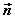 的夹角为 的夹角为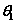 ,直线L与平面 ,直线L与平面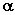 所成的角为 所成的角为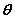 ,则 ,则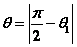 , ,
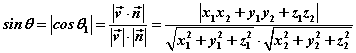 。 。
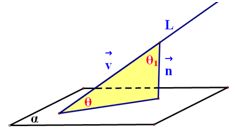
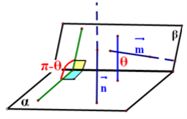
⑻求空间二面角:
设平面α的法向量为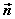 ,平面β的法向量为 ,平面β的法向量为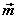 ,向量 ,向量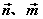 所成的角为 所成的角为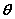 , ,
若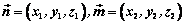 , ,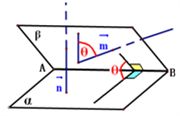
则
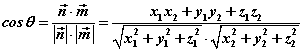 。 。
那么二面角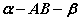 的大小为 的大小为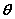 或 或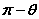 ,视具体情况而定(如图)。 ,视具体情况而定(如图)。
空间向量数量积运算<-->空间向量基本定理
全网搜索"空间向量数量积运算的应用"相关
|

