|
14.2.1空间直角坐标系<-->14.2.3夹角和距离公式
空间向量的坐标表示
Ⅰ、空间直角坐标系:
⑴若空间的一个基底的三个基向量互相垂直,且长为1,这个基底叫单位正交基底,用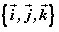 表示。 表示。
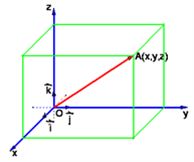
⑵在空间选定一点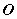 和一个单位正交基底 和一个单位正交基底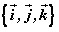 ,以点 ,以点 为原点,分别以 为原点,分别以
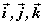 的方向为正方向建立 的方向为正方向建立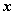 轴、 轴、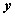 轴、 轴、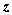 轴三个坐标轴.则称建立了一个空间 轴三个坐标轴.则称建立了一个空间
直角坐标系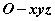 ,点 ,点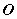 叫原点,向量 叫原点,向量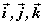 都叫坐标向量.通过每两个坐标 都叫坐标向量.通过每两个坐标
轴的平面叫坐标平面,分别称为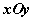 平面, 平面,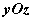 平面, 平面,  平面。 平面。
Ⅱ、空间直角坐标系中的坐标:
在空间直角坐标系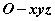 中,对空间任一点 中,对空间任一点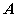 ,存在唯一的有序实数组 ,存在唯一的有序实数组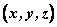 ,使 ,使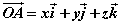 ,有序实数组 ,有序实数组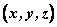 叫作向量 叫作向量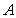 在空间直角坐标系 在空间直角坐标系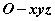 中的坐标,记作 中的坐标,记作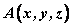 , , 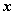 叫横坐标, 叫横坐标, 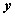 叫纵坐标, 叫纵坐标, 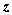 叫竖坐标。 叫竖坐标。
显然,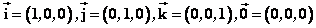 。 。
Ⅲ、向量坐标表示的说明:
⑴向量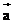 与有序实数对 与有序实数对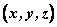 一一对应。 一一对应。
⑵向量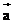 的坐标与表示该向量的有向线段的起点、终点的具体位置没有关系,只与其相对位置有关系。 的坐标与表示该向量的有向线段的起点、终点的具体位置没有关系,只与其相对位置有关系。
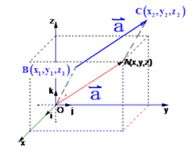
如图,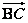 是表示向量 是表示向量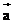 的有向线段,若点B、C的坐标分别为 的有向线段,若点B、C的坐标分别为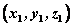 , ,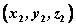 ,则向量 ,则向量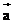 的坐标为: 的坐标为: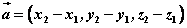 。 。
⑶若把坐标原点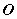 作为表示向量 作为表示向量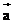 的有向线段的起点,则向量 的有向线段的起点,则向量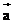 的坐标就由表示向量 的坐标就由表示向量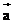 的有向线段的终点坐标唯一确定,即点A的坐标就是向量 的有向线段的终点坐标唯一确定,即点A的坐标就是向量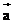 的坐标。即 的坐标。即
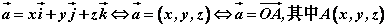 。 。
⑷若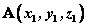 , ,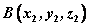 ,则 ,则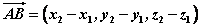 。即一个向量在直角坐标系中的坐标等于表示这个向量的有向线段的终点的坐标减去起点的坐标。 。即一个向量在直角坐标系中的坐标等于表示这个向量的有向线段的终点的坐标减去起点的坐标。
⑸线段的中点坐标:
若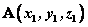 , ,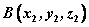 ,则线段AB的中点坐标为 ,则线段AB的中点坐标为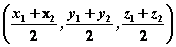 。 。
即线段的中点坐标等于线段两端点坐标的平均值。
空间向量的坐标运算
Ⅰ、空间向量的坐标运算:
设向量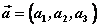 , , ,则 ,则
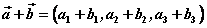 , ,
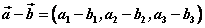 , ,
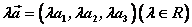 。 。
即两个向量和(差)的坐标分别等于这两个向量相应坐标的和(差);实数与向量的积的坐标等于用这个实数乘原来向量的相应坐标。
Ⅱ、向量模的坐标运算:
将向量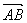 平移,使得点A与坐标原点O重合,则平移后的B点位置就是P点。向量 平移,使得点A与坐标原点O重合,则平移后的B点位置就是P点。向量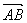 的坐标是以原点为始点,点P为终点的向量坐标,这样就建立了向量的坐标与点的坐标之间的联系。因此,向量 的坐标是以原点为始点,点P为终点的向量坐标,这样就建立了向量的坐标与点的坐标之间的联系。因此,向量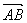 的模与向量 的模与向量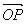 的模是相等的。由此可得向量模的坐标运算公式,即平面内两点间的距离公式: 的模是相等的。由此可得向量模的坐标运算公式,即平面内两点间的距离公式:
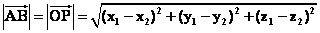 。 。
Ⅲ、向量坐标与有向线段始终点坐标的关系:
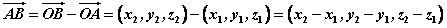 。 。
即一个向量的坐标等于表示此向量的有向线段的终点的坐标减去始点的坐标。
14.2.1空间直角坐标系<-->14.2.3夹角和距离公式
全网搜索"14.2.2空间向量的坐标运算"相关
|

