|
8.2.1平面向量的基本定理<-->8.2.3平面向量的坐标运算
向量的夹角
〖定义〗如图,已知两个非零向量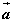 和b,作 和b,作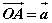 , ,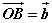 ,则 ,则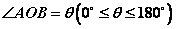 叫做向量 叫做向量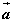 与 与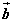 的夹角。 的夹角。
夹角的范围:两非零向量夹角的范围在区间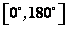 内。 内。
〖代数表示〗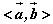
〖几何表示〗
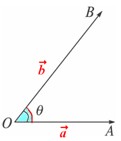
详解:
〖记忆方法〗首首相连,所成即角。
〖概念辨析〗注意用来表示向量的两条有向线段的起点要放一起。
向量的正交分解
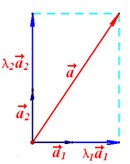
〖向量的正交分解〗若不共线的两个向量相互垂直,由平面向量的基本定理,对平面上的任意向量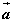 ,均可以分解为两个互相垂直的向量 ,均可以分解为两个互相垂直的向量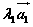 和 和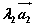 ,使 ,使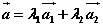 。这样把一个向量分解为两个互相垂直的向量,叫做把向量正交分解。 。这样把一个向量分解为两个互相垂直的向量,叫做把向量正交分解。
正交分解是向量分解中非常重要的一种,它构建了平面向量及其运算的坐标表示。
〖几何表示〗
平面向量的坐标表示
〖形成〗
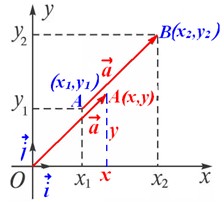
如图,在平面直角坐标系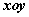 中,分别取与 中,分别取与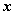 轴、 轴、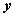 轴方向相同的两个单位向量 轴方向相同的两个单位向量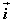 、 、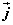 作为基底。对于平面内的一个向量 作为基底。对于平面内的一个向量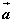 ,由平面向量基本定理可知,有且只有一对实数 ,由平面向量基本定理可知,有且只有一对实数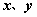 ,使得 ,使得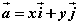 。 。
这样,平面内的任一向量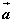 都可由 都可由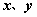 唯一确定,我们把有序数对 唯一确定,我们把有序数对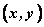 叫做向量 叫做向量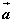 的坐标,记作 的坐标,记作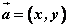 。 。
其中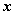 叫做 叫做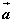 在 在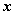 轴上的坐标, 轴上的坐标,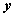 叫做 叫做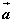 在 在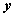 轴上的坐标,式子 轴上的坐标,式子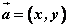 叫做向量的坐标表示。 叫做向量的坐标表示。
显然,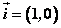 , ,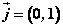 , ,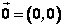 。 。
〖代数表示〗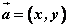
〖几何表示〗
|

