|
2022年高考数学上海14<-->2022年高考数学上海16
(5分)如图正方体ABCD−A1B1C1D1中,P、Q、R、S分别为棱AB、BC、BB1、CD的中点,联结A1S,B1D.空间任意两点M、N,若线段MN上不存在点在线段A1S、B1D上,则称MN两点可视,则下列选项中与点D1可视的为( )
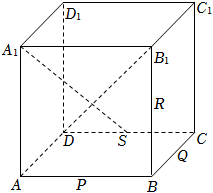
A.点P B.点B C.点R D.点Q
分析:线段MN上不存在点在线段A1S、B1D上,即直线MN与线段A1S、B1D不相交,因此所求与D1可视的点,即求哪条线段不与线段A1S、B1D相交,再利用共面定理,异面直线的判定定理即可判断.
解:线段MN上不存在点在线段A1S、B1D上,即直线MN与线段A1S、B1D不相交,
因此所求与D1可视的点,即求哪条线段不与线段A1S、B1D相交,
对A选项,如图,连接A1P、PS、D1S,因为P、S分别为AB、CD的中点,
∴易证A1D1//PS,故A1、D1、P、S四点共面,∴D1P与A1S相交,∴A错误;

对B、C选项,如图,连接D1B、DB,易证D1、B1、B、D四点共面,
故D1B、D1R都与B1D相交,∴B、C错误;
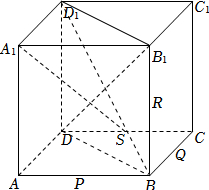
对D选项,连接D1Q,由A选项分析知A1、D1、P、S四点共面记为平面A1D1PS,
∵D1∈平面A1D1PS,Q∉平面A1D1PS,且A1S⊂平面A1D1PS,点D1∉A1S,
∴D1Q与A1S为异面直线,
同理由B,C选项的分析知D1、B1、B、D四点共面记为平面D1B1BD,
∵D1∈平面D1B1BD,Q∉平面D1B1BD,且B1D⊂平面D1B1BD,点D1∉B1D,
∴D1Q与B1D为异面直线,
故D1Q与A1S,B1D都没有公共点,∴D选项正确.

故选:D.
点评:本题考查新定义,共面定理的应用,异面直线的判定定理,属中档题.
2022年高考数学上海14<-->2022年高考数学上海16
全网搜索"2022年高考数学上海15"相关
|

