|
2020年高考数学全国卷Ⅱ--理8<-->2020年高考数学全国卷Ⅱ--理10
(2020新课标Ⅱ卷单选题)
设函数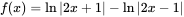 ,则 ,则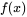 ( )。 ( )。
【A】是偶函数,且在 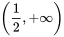 上单调递增
【B】是奇函数,且在 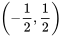 上单调递减
【C】是偶函数,且在 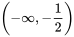 上单调递增
【D】是奇函数,且在 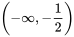 上单调递减
【出处】
2020年普通高等学校招生全国统一考试(新课标Ⅱ卷):理数第9题
【解析】
本题主要考查函数的概念与性质。
函数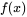 的定义域为 的定义域为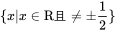 ,关于原点对称。 ,关于原点对称。
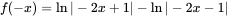 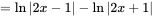 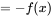 , ,
所以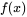 是奇函数。 是奇函数。
①当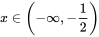 时, 时,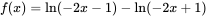 。 。
求导得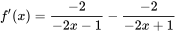
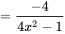 。 。
因为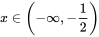 , ,
所以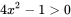 , ,
所以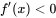 。 。
所以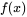 在 在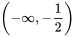 上单调递减。 上单调递减。
②当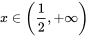 时, 时,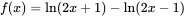 。 。
求导得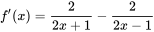
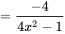 。 。
因为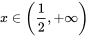 , ,
所以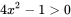 , ,
所以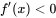 。 。
所以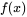 在 在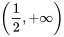 上单调递减。 上单调递减。
③当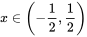 时, 时,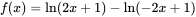 。 。
求导得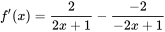
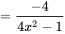 。 。
因为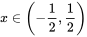 , ,
所以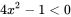 , ,
所以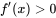 。 。
所以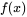 在 在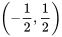 上单调递增。 上单调递增。
故本题正确答案为D。 【考点】
函数的概念与性质函数的单调性函数的奇偶性 2020年高考数学全国卷Ⅱ--理8<-->2020年高考数学全国卷Ⅱ--理10
全网搜索"2020年高考数学全国卷Ⅱ--理9"相关
|

