(29)本小题考查一元二次方程根与系数的关系，

绝对值不等式的性质和证明；逻辑推理能力和

分析问题、解决问题的能力。

证法一：

依题设，二次方程有两个实根α，β，所以判别式

不妨取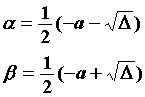

 (Ⅰ)∵　|α|＜2，|β|＜2。∴|b|=|αβ|=|α|·|β|＜4

　　　　　

　　　　

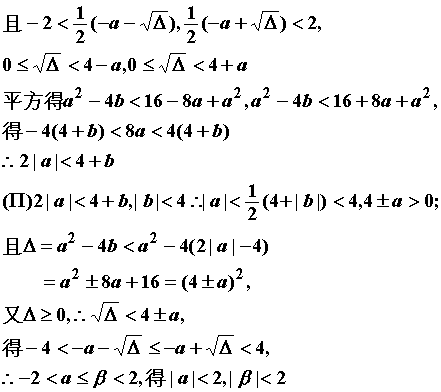
证法二：

(Ⅰ)根据韦达定理|b|=|αβ|＜4。

因为二次函数f(x)=x2+ax+b开口向上，|α|＜2，|β|＜2。

故必有f(±2)＞0，

即4+2a+b＞0，2a＞-(4+b);

4-2a+b＞0，2a＜4+b。

∴2|a|＜4+b。

(Ⅱ)由2|a|＜4+b得4+2a+b＞0即22+2a+b＞0，f(2)＞0。①

及4-2a+b＞0即(-2)2+(-2)a+b＞0，f(-2)＞0。　②

由此可知f(x)=0的每个实根或者在区间(-2，2)之内

或者在(-2，2)之外。

若两根α,β均落在(-2，2)之外，则与|b|=|αβ|＜4矛盾。

若α(或β)落在(-2，2)外，则由于|b|=|αβ|＜4，

另一个根β(或α)必须落在(-2，2)内，

则与①，②式矛盾。

综上所述α，β均落在(-2，2)内。

∴|α|＜2，|β|＜2。