|
一、复习目标 理解空间向量坐标的概念,掌握空间向量的坐标运算;掌握用直角坐标计算空间向量数量积的公式;掌握空间两点间距离公式. 会用上述知识解决立体几何中有关的简单问题.
二、重点难点 三、特别提示
(2)用向量方法解决立体几何问题时,关键是一个几何问题向量化的转化过程,从建立基向量,到表示相关向量,到应用向量的有关运算,到结论得出,构成一个非常严密的解(证)题过程,这也代表着立体几何的一个发展趋势.
(3)运用空间向量的坐标运算解决立体几何问题时,一般步骤为: ①建立恰当的空间直角坐标系(例如:底面是矩形的直四棱柱,以底面其中一个顶点为原点建立空间直角坐标系;底面是菱形的直四棱柱,往往以底面对角线交点为原点建立空间直角坐标系); ②求出相关点的坐标; ③写出向量的坐标; ④结合公式进行论证,计算; ⑤转化为几何结论. 建立空间直角坐标系,必须牢牢抓住相交于同—点的两两垂直的三条直线,要在题目中找出或构造出这样的三条直线,因此,要充分利用题目中所给的垂直关系(即线线垂直、线面垂直、面面垂直),同时要注意,所建立的坐标系必须是右手空间直角坐标系.
(4)借助空间向量可将立体几何中的平行、垂直、夹角、距离等问题转化为向量的坐标运算. ①平行问题向量共线,注意重合; ②垂直问题向量的数量积为零,注意零向量; ③距离问题向量的模,注意向量的垂直; ④求角问题向量的夹角,注意角范围的统一. |
|
知识梳理 1、空间向量的有关概念 (1)把具有大小和方向的量叫做向量,其长度叫做空间向量的模. (2)同向且等长的有向线段表示同一向量或相等的向量.
2、空间向量的加法与数乘向量运算的运算律: (3)数乘分配律:
3、共线向量与共面向量 推论:如果为经过已知点平行于已知非零向量的直线,那么,对任一点,点在直线的充要条件是存在实数,满足等式,其中向量叫做直线的方向向量.
(2)共面向量定理:如果两个向量不共线,则向量与向量共面的充要条件是存在实数对,使. 推论:空间一点位于平面内的充分必要条件是存在有序数对,使,或对空间任一定点,有.
4、空间向量基本定理:如果三个向量不共面,那么对空间任一向量,存在一个唯一有序实数对、、,使.由此可知,如果三个向量、、不共面,那么所有空间问量所组成的集合就是,这个集合可看作是由向量、、生成的,把叫做空间的一个基底,、、都叫做基向量. 推论:设是不共面的四点,则对空间任一点,都存在唯一有序实数对,使.
5、两个向量的数量积
(2)空间向量数量积的性质: ① ② ③
(3)空间向量数量积的运算律: ① ②(交换律) ③(分配律)
6、空间直角坐标系 (1)如果空间的一个基底的三个基向量互相垂直,且长度为1,则这个基底叫做单位正交基底.
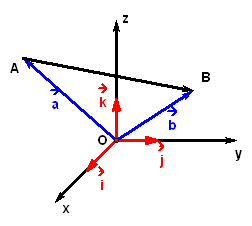
(2)在空间直角坐标系中,让右手拇指指向轴的正方向,食指指向轴的正方向,如果中指能指向轴的正方向,则称这个坐标系为右手直角坐标系.
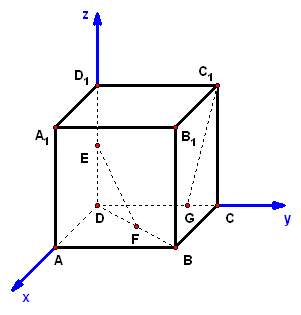
(3)如图,为坐标向量(单位向量、正交基底),对于空间任一点,对应一个向量,于是存在唯一的唯一有序实数对、、,使,这个数组叫做点在空间直角坐标系下的坐标,记作.
8、在空间直角坐标系中,已知,, 则, 其中表示与两点间的距离,这就是空间两点间的距离公式. |
|
应用举例
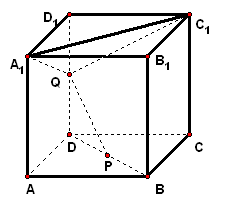
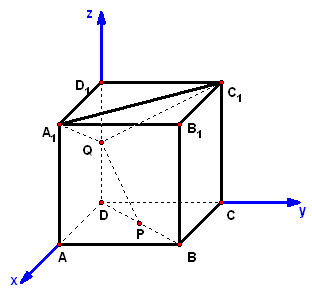
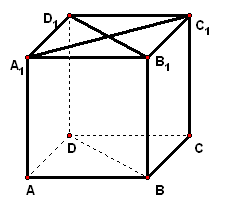
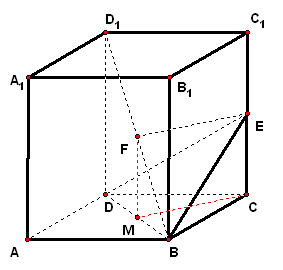
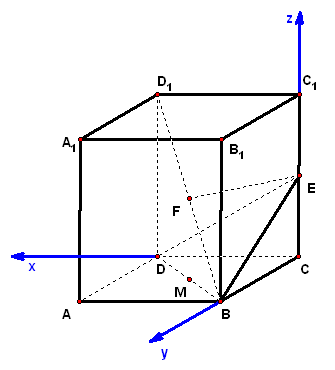
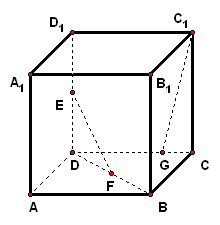
二、案例示范 1、已知正方体,为底面对角线上一点且,为棱的中点,试证:平面
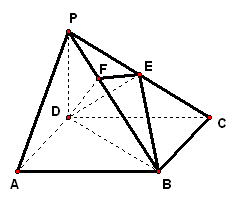
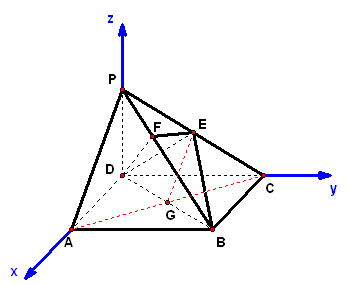
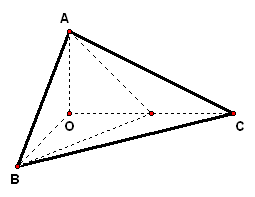
2、如图,在四棱锥中,底面是正方形,侧棱,,的中点,作交
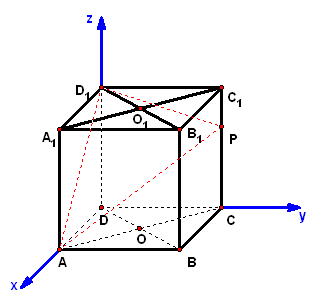
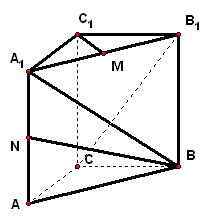
3、(06·湖北)如图,在棱长为的正方体中,是侧棱上的一点,
|
| 实践体验 在实践中提高能力,在体验中反思感悟,力求独立,力求提高 1、正四棱柱,,,点为的中点,点是的中点
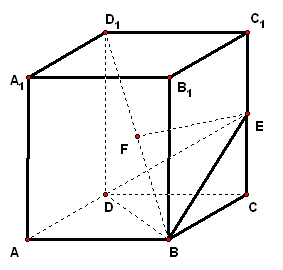
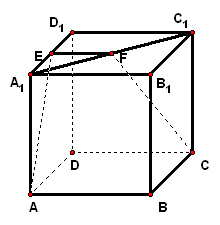
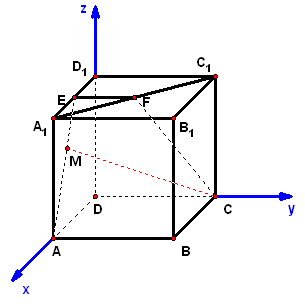
2、已知正方体中,分别是的中点,求
|
|
拓展探究
|
|
|
|
|
学习感悟
2、共线与共面向量不具有传递性.
3、应用向量基本定理和向量数量积可以用于解决向量相等、垂直、夹角等问题. 用向量解决立体几何的问题,关键是要找到几何问题的向量表示,然后将题设条件向量化,用已知向量表示出未知向量,从而转化为已知向量间的问题.根据空间向量基本定理,如果已知向量中有三个不共面的,则可以由此构成一个空间基底,其它任何向量都可以用基向量唯一表示出来,从而进行运算 .线共点、线共面、线线垂直、两异面直线所成的角、两点间的距离等等,都可由此解决.
4、在应用向量数量积求异面直线所成角或线面角、二面角等问题时应结合实际,合理取舍和转化,避免出现所求值与角的范围不一致的现象.
5、(1)在空间图形中,如果线段较多,关系也较为复杂(如平行、垂直、角和距离等均有涉及),此时如何入手,是用传统方法解决,还是用向量方法解决,一般较难作出判断,而且在较为综合的问题中,只用某一种方法,有时也难以奏效,常常需要多种方法灵活使用,合理结合,才能达到理想效果. (2)图形中如果存在三条两两垂直的线段,则可考虑以它们所在直线为坐标轴建立空间直角坐标系,设法确定点、向量的坐标,然后通过向量的坐标,利用向量坐标运算解决有关问题 .解题中应注意逻辑推导和向量运算的有机结合. (3)利用向量的坐标解决立体几何中的平行、垂直、求解、求距离等问题,关键是建立正确的空间直角坐标系,难点是正确表示已知点的坐标;对空间任意一点,求其坐标的一般方法:过作轴的平行线交平面于,过分别作轴的平行线,分别交轴于,则由,,的长度和方向便可求得点的坐标. |