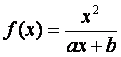 (a,b为常数)且方程f(x)-x+12=0有两个实根
(a,b为常数)且方程f(x)-x+12=0有两个实根2005年
解答题
17.(本小题满分12分)
已知函数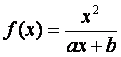 (a,b为常数)且方程f(x)-x+12=0有两个实根
(a,b为常数)且方程f(x)-x+12=0有两个实根
为x1=3, x2=4.
(1)求函数f(x)的解析式;
(2)设k>1,解关于x的不等式;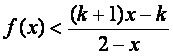
18.(本小题满分12分)
已知向量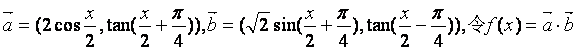 .
.
是否存在实数![]()
若存在,则求出x的值;若不存在,则证明之.
19.(本小题满分12分)
A、B两位同学各有五张卡片,现以投掷均匀硬币的形式进行游戏,当出现正面
朝上时A赢得B一张卡片,否则B赢得A一张卡片.规定掷硬币的次数达9次时,或
在此前某人已赢得所有卡片时游戏终止.设![]() 表示游戏终止时掷硬币的次数.
表示游戏终止时掷硬币的次数.
(1)求![]() 的取值范围;
的取值范围;
(2)求![]() 的数学期望E
的数学期望E![]() .
.
20.(本小题满分12分)
如图,在长方体ABCD—A1B1C1D1,中,AD=AA1=1,AB=2,点E在棱AB上移动.
(1)证明:D1E⊥A1D;
(2)当E为AB的中点时,求点E到面ACD1的距离;
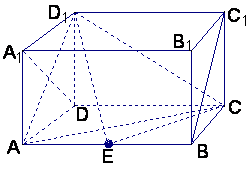 (3)AE等于何值时,二面角D1—EC—D的大小为
(3)AE等于何值时,二面角D1—EC—D的大小为![]() .
.
21.(本小题满分12分)
已知数列![]()
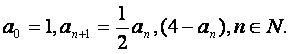
(1)证明![]()
(2)求数列![]() 的通项公式an.
的通项公式an.
22.(本小题满分14分)
设抛物线![]() 的焦点为F,动点P在直线
的焦点为F,动点P在直线![]() 上运动,
上运动,
过P作抛物线C的两条切线PA、PB,且与抛物线C分别相切于A、B两点.
(1)求△APB的重心G的轨迹方程.
(2)证明∠PFA=∠PFB.
2006
解答题17.(本小题满分12分)
已知函数f(x)=x3+ax2+bx+c在x=-![]() 与x=1时都取得极值.
与x=1时都取得极值.
(1)求a、b的值及函数f(x)的单调区间;
(2)若对x∈[-1,2],不等式f(x)<c2恒成立,求c的取值范围.
18.(本小题满分12分)
某商场举行抽奖促销活动,抽奖规则是:从装有9个白球、1个红球的箱子中每
次随机地摸出一个球,记下颜色后放回,摸出一个红球可获得奖金10元;摸出两个红
球可获得奖金50元.现有甲、乙两位顾客,规定:甲摸一次,乙摸两次.令ξ表示甲、
乙两人摸球后获得的奖金总额.求
(1)ξ的分布列; (2)ξ的数学期望.
19.(本小题满分12分)
如图,已知△ABC是边长为1的正三角形,M、N分别是边AB、AC上的
点,线段MN经过△ABC的中心G.设∠MGA=α(![]() ≤α≤
≤α≤![]() ).
).
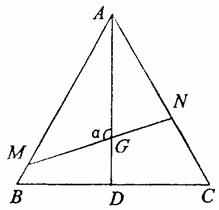
(1)试将△AGM、△AGN的面积(分别记为S1与S2)表示为α的函数;
(2)求y=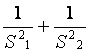 的最大值与最小值.
的最大值与最小值.
20.(本小题满分12分)
如图,在三棱锥A-BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜边,
且AD=![]() ,BD=CD=1.另一个侧面ABC是正三角形.
,BD=CD=1.另一个侧面ABC是正三角形.
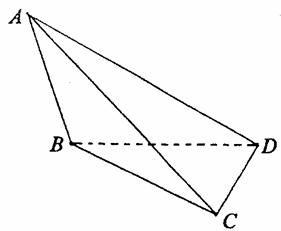
(1)求证:AD⊥BC;
(2)求二面角B-AC-D的大小;
(3)在线段AC上是否存在一点E,使ED与面BCD成30°角?若存在,确定点E的位置;
若不存在,说明理由.
21.(本小题满分12分)
如图,椭圆Q: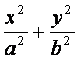 =1(a>b>0)的右焦点为F(c,0),过点F的一动直线m绕
=1(a>b>0)的右焦点为F(c,0),过点F的一动直线m绕
点F转动,并且交椭圆于A、B两点,P为线段AB的中点.
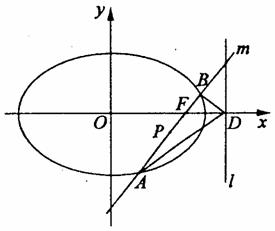
(1)求点P的轨迹H的方程;
(2)若在Q的方程中,令a2=1+cosθ+sinθ,b2=sinθ(0<θ≤![]() ).确定θ的值,使
).确定θ的值,使
原点距椭圆Q的右准线l最远.此时,设l与x轴交点为D,当直线m绕点F转动到
什么位置时,三角形ABD的面积最大?
22.(本小题满分14分)
已知数列{an}满足:a1=![]() ,且an=
,且an= (n≥2,n∈N*).
(n≥2,n∈N*).
(1)求数列{an}的通项公式;
(2)证明:对一切正整数n,不等式a1·a2·…·an<2·n!恒成立.
2007年
解答题
17.(本小题满分12分)
已知函数 在区间
在区间![]() 内连续,且
内连续,且![]() .
.
(1)求实数![]() 和
和![]() 的值;
的值;
(2)解不等式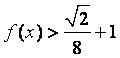 .
.
18.(本小题满分12分)
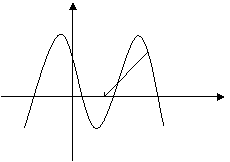 如图,函数
如图,函数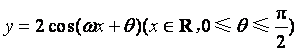 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,
,
且在该点处切线的斜率为![]() .
.
(1)求![]() 和
和![]() 的值;
的值;
![]()
(2)已知点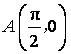 ,点
,点![]() 是该函数图象上一点,
是该函数图象上一点,
点![]() 是
是![]() 的中点,当
的中点,当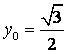 ,
,![]() 时,求
时,求![]() 的值.
的值.
19.(本小题满分12分)
某陶瓷厂准备烧制甲、乙、丙三件不同的工艺品,制作过程必须先后经过两次
烧制,当第一次烧制合格后方可进入第二次烧制,两次烧制过程相互独立.根
据该厂现有的技术水平,经过第一次烧制后,甲、乙、丙三件产品合格的概率
依次为![]() ,
,![]() ,
,![]() ,经过第二次烧制后,甲、乙、丙三件产品合格的概率依
,经过第二次烧制后,甲、乙、丙三件产品合格的概率依
次为![]() ,
,![]() ,
,![]() .
.
(1)求第一次烧制后恰有一件产品合格的概率;
(2)经过前后两次烧制后,合格工艺品的个数为![]() ,求随机变量
,求随机变量![]() 的期望.
的期望.
20.(本小题满分12分)
 右图是一个直三棱柱(以
右图是一个直三棱柱(以![]() 为底面)被一平面所截得到的几何体,截面为
为底面)被一平面所截得到的几何体,截面为![]() .
.
已知![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)设点![]() 是
是![]() 的中点,证明:
的中点,证明:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的大小;
的大小;
(3)求此几何体的体积.
21.(本小题满分12分)
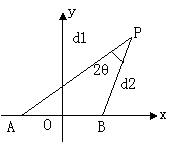 设动点
设动点![]() 到点
到点![]() 和
和![]() 的距离分别为
的距离分别为![]() 和
和![]() ,
,![]() ,且存在常数
,且存在常数![]() ,
,
使得![]() .
.
(1)证明:动点![]() 的轨迹
的轨迹![]() 为双曲线,并求出
为双曲线,并求出![]() 的方程;
的方程;
(2)过点![]() 作直线双曲线
作直线双曲线![]() 的右支于
的右支于![]() 两点,
两点,
试确定![]() 的范围,使
的范围,使![]() ,其中点
,其中点![]() 为坐标原点.
为坐标原点.
22.(本小题满分14分)
设正整数数列![]() 满足:
满足:![]() ,且对于任何
,且对于任何![]() ,有
,有 .
.
(1)求![]() ,
,![]() ;
;
(3)求数列![]() 的通项
的通项![]() .
.
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。