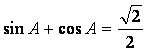 ,
,2004年
解答题
(15)(本小题满分13分)
在![]() 中,
中,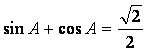 ,
,![]() ,
,![]() ,求
,求![]() 的值和
的值和![]() 的面积
的面积
(16)(本小题满分14分)
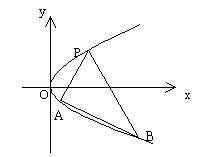
如图,在正三棱柱![]() 中,AB=3,
中,AB=3,![]() ,M为
,M为![]() 的中点,P是BC上一点,
的中点,P是BC上一点,
且由P沿棱柱侧面经
过棱![]() 到M的最短路线长为
到M的最短路线长为![]() ,设这条最短路线与
,设这条最短路线与![]() 的交点为N,
的交点为N,
求:
(I)该三棱柱的侧面展开图的对角线长
(II)PC和NC的长
(III)平面NMP与平面ABC所成二面角(锐角)的大小(用反三角函数表示)
(17)(本小题满分14分)
如图,过抛物线![]() 上一定点P(
上一定点P(![]() )(
)(![]() ),作两条直线
),作两条直线
分别交抛物线于A(![]() ),B(
),B(![]() )
)
(I)求该抛物线上纵坐标为![]() 的点到其焦点F的距离
的点到其焦点F的距离
(II)当PA与PB的斜率存在且倾斜角互补时,求![]() 的值,并证明直线AB
的值,并证明直线AB
的斜率是非零常数
(18)(本小题满分14分)
函数![]() 是定义在[0,1]上的增函数,满足
是定义在[0,1]上的增函数,满足![]() 且
且![]() ,
,
在每个区间![]() (
(![]() 1,2……)
上,
1,2……)
上,![]() 的图象都是斜率为同一常数k的
的图象都是斜率为同一常数k的
直线的一部分。
(I)求![]() 及
及![]() ,
,![]() 的值,并归纳出
的值,并归纳出![]() 的表达式
的表达式
(II)设直线![]() ,
,![]() ,x轴及
,x轴及![]() 的图象围成的矩形的面积为
的图象围成的矩形的面积为
![]() (
(![]() 1,2……),记
1,2……),记![]() ,求
,求![]() 的表达式,并写出其定义域和最小值
的表达式,并写出其定义域和最小值
(19)(本小题满分12分)
某段城铁线路上依次有A、B、C三站,AB=15km,BC=3km,在列车运行
时刻表上,规定列车8时整从A站发车,8时07分到达B站并停车1分钟,8时12分
到达C站,在实际运行中,假设列车从A站正点发车,在B站停留1分钟,并在行
驶时以同一速度![]() 匀速行驶,列车从A站到达某站的时间与时刻表上相应时
匀速行驶,列车从A站到达某站的时间与时刻表上相应时
间之差 的绝对值称为列车在该站的运行误差。
(I)分别写出列车在B、C两站的运行误差
(II)若要求列车在B,C两站的运行误差之和不超过2分钟,求![]() 的取值范围
的取值范围
(20)(本小题满分13分)
给定有限个正数满足条件T:每个数都不大于50且总和L=1275。现将这些数按
下列要求进行分组,每
组数之和不大于150且分组的步骤是:
首先,从这些数中选择这样一些数构成第一组,使得150与这组数之和的差![]() 与
与
所有可能的其他选择相
比是最小的,![]() 称为第一组余差;
称为第一组余差;
然后,在去掉已选入第一组的数后,对余下的数按第一组的选择方式构成第二组,
这时的余差为![]() ;
如此继续构成第三组(余差为
;
如此继续构成第三组(余差为![]() )、第四组(余差为
)、第四组(余差为![]() )、……,
)、……,
直至第N组(余差为![]() )把这些数全部分
完为止。
)把这些数全部分
完为止。
(I)判断![]() 的大小关系,并指出除第N组外的每组至少含有几个数
的大小关系,并指出除第N组外的每组至少含有几个数
(II)当构成第n(n<N)组后,指出余下的每个数与![]() 的大小关系,
的大小关系,
并证明![]()
(III)对任何满足条件T的有限个正数,证明:![]()
2005年
解答题
15 (本小题共13分)
已知函数![]()
![]()
(I)求![]() 的单调递减区间;
的单调递减区间;
(Ⅱ)若![]() 在区间[一2,2]上的最大值为20,求它在该区间上的最小值
在区间[一2,2]上的最大值为20,求它在该区间上的最小值![]()
16 (本小题共14分)
如图,在直四棱柱![]() 中,
中,![]() ,
,
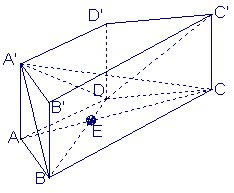
![]() 垂足为
垂足为![]()
![]()
(Ⅰ)求证![]() ;
;
(Ⅱ)求二面角![]() 的大小;
的大小;
(Ⅲ)求异面直线![]() 与
与![]() 所成角的大小
所成角的大小![]()
17 (本小题共13分)
甲、乙俩人各进行3次射击,甲每次击中目标的概率为![]() ,乙每次击中目标的概率为
,乙每次击中目标的概率为![]()
![]()
(Ⅰ)记甲击中目标的次数为![]() ,求
,求![]() 的概率分布及数学期望
的概率分布及数学期望![]() ;
;
(Ⅱ)求乙至多击中目标2次的概率;
(Ⅲ)求甲恰好比乙多击中目标2次的概率![]()
18 (本小题共14分)
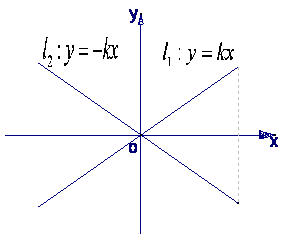 如图,直线
如图,直线![]() 与直线
与直线![]() 之间的阴影区域(不含边界)记为
之间的阴影区域(不含边界)记为![]() ,
,
其左半部分记为![]() ,右半部分记为
,右半部分记为![]()
![]()
(Ⅰ)分别有不等式组表示![]() 和
和![]()
![]()
(Ⅱ)若区域![]() 中的动点
中的动点![]() 到
到![]() 的距离
的距离
之积等于![]() ,求点
,求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅲ)设不过原点![]() 的直线
的直线![]() 与(Ⅱ)中的曲线
与(Ⅱ)中的曲线![]()
相交于![]() 两点,且与
两点,且与![]() 分别交于
分别交于![]() 两点.
两点.
求证△![]() 的重心与△
的重心与△![]() 的重心重合
的重心重合![]()
19 (本小题共12分)
设数列![]() 的首项
的首项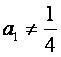 ,且
,且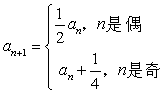 ,记
,记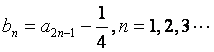
![]()
(Ⅰ)求![]()
(Ⅱ)判断数列![]() 是否为等比数列,并证明你的结论;
是否为等比数列,并证明你的结论;
(Ⅲ)求![]()
![]()
20 (本小题共14分)
设![]() 是定义在[0,1]上的函数,若存在
是定义在[0,1]上的函数,若存在![]() ,使得
,使得![]() 在[0,
在[0,![]() ]上
]上
单调递增,在[![]() ,1]单调递减,则称
,1]单调递减,则称![]() 为[0,1]上的单峰函数,
为[0,1]上的单峰函数,![]() 为峰点,
为峰点,
包含峰点的区间为含峰区间![]()
对任意的[0,1]上的单峰函数![]() ,下面研究缩短其含峰区间长度的方法
,下面研究缩短其含峰区间长度的方法![]()
(Ⅰ)证明:对任意的![]()
![]() ,
, ![]() ,若
,若![]() ,则(0,
,则(0,![]() )为
)为
含峰区间;若![]() ,则(
,则(![]() ,1)为含峰区间;
,1)为含峰区间;
(Ⅱ)对给定的![]() (0<
(0<![]() <0.5),证明:存在
<0.5),证明:存在![]()
![]() ,满足
,满足![]() ,
,
使得由(Ⅰ)确定的含峰区间的长度不大于0.5+![]() ;
;
(Ⅲ)选取![]()
![]() ,
,![]() 由(Ⅰ)可确定含峰区间为(0,
由(Ⅰ)可确定含峰区间为(0,![]() )或(
)或(![]() ,1),
,1),
在所得的含峰区间内选取![]() ,由
,由![]() 与
与![]() 或
或![]() 与
与![]() 类似地可确定是一个新的含峰区间.
类似地可确定是一个新的含峰区间.
在第一次确定的含峰区间为(0,![]() )的情况下,试确定
)的情况下,试确定![]() 的值,满足两两
的值,满足两两
之差的绝对值不小于0.02且使得新的含峰区间的长度缩短到0.34![]()
(区间长度等于区间的右端点与左端点之差)![]()
2006年
解答题
(15)(本小题共12分)
已知函数f(x)=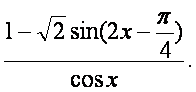
(Ⅰ)求f(x)的定义域;
(Ⅱ)设α是第四象限的角,且tanα=-![]() 求f(α)的值.
求f(α)的值.
(16)(本小题共13分)
已知函数f(x)=ax3+bx2+cx在点x0处取得极大值5,其导函数y=f′(x)
的图象经过点(1,0),(2,0),如图所示,求:
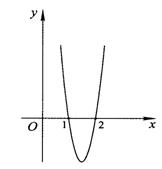
(Ⅰ)x0的值;
(Ⅱ)a,b,c的值.
(17)(本小题共14分)
如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,
且PA=AB,点E是PD的中点.
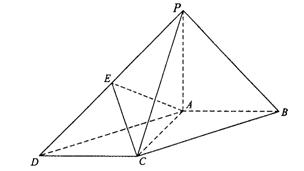
(Ⅰ)求证:AC⊥PB;
(Ⅱ)求证:PB∥平面AEC;
(Ⅲ)求二面角E-AC-B的大小.
(18)(本小题共13分)
某公司招聘员工,指定三门考试课程,有两种考试方案.
方案一:考试三门课程,至少有两门及格为考试通过;
方案二:在三门课程中,随机选取两门,这两门都及格为考试通过.
假设某应聘者对三门指定课程考试及格的概率分别是a,b,c,且三门课程
考试是否及格相互之间没有影响.
(Ⅰ)分别求该应聘者用方案一和方案二时考试通过的概率;
(Ⅱ)试比较该应聘者在上述两种方案下考试通过的概率的大小.(说明理由)
(19)(本小题共14分)
已知点M(-2,0),N(2,0),动点P满足条件|PM|-|PN|=2![]() .记动点P的
.记动点P的
轨迹为W.
(Ⅰ)求W的方程;
(Ⅱ)若A,B是W上的不同两点,O是坐标原点,求![]() 的最小值.
的最小值.
(20)(本小题共14分)
在数列{an}中,若a1,a2是正整数,且an=|an-1-an-2|,n=3,4,5,…,
则称{an}为“绝对差数列”.
(Ⅰ)举出一个前五项不为零的“绝对差数列”(只要求写出前十项);
(Ⅱ)若“绝对差数列”{an}中,a20=3,a21=0,数列{bn}满足bn=an+ an+1
+ an+2,n=1,2,3,…,分别判断当n→∞时,an与bn的极限是否存在,如果存
在,求出其极限值;
(Ⅲ)证明:任何“绝对差数列”中总含有无穷多个为零的项.
2007年
解答题
15.(本小题共13分)
数列![]() 中,
中,![]() ,
,![]() (
(![]() 是常数,
是常数,![]() ),
),
且![]() 成公比不为
成公比不为![]() 的等比数列.
的等比数列.
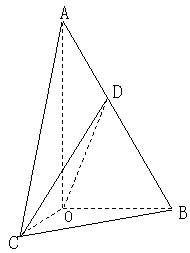 (I)求
(I)求![]() 的值;
的值;
(II)求![]() 的通项公式.
的通项公式.
16.(本小题共14分)
如图,在![]() 中,
中,![]() ,斜边
,斜边![]() .
.![]() 可以通过
可以通过![]() 以
以
直线![]() 为轴旋转得到,且二面角
为轴旋转得到,且二面角![]() 是直二面角.动点
是直二面角.动点![]() 的斜边
的斜边![]() 上.
上.
(I)求证:平面![]() 平面
平面![]() ;
;
(II)当![]() 为
为![]() 的中点时,求异面直线
的中点时,求异面直线![]() 与
与![]() 所成角的大小;
所成角的大小;
(III)求![]() 与平面
与平面![]() 所成角的最大值.
所成角的最大值.
17.(本小题共14分)
矩形![]() 的两条对角线相交于点
的两条对角线相交于点![]() ,
,![]() 边所在直线的方程为
边所在直线的方程为![]() ,
,
点![]() 在
在![]() 边所在直线上.
边所在直线上.
(I)求![]() 边所在直线的方程;
边所在直线的方程;
(II)求矩形![]() 外接圆的方程;
外接圆的方程;
(III)若动圆![]() 过点
过点![]() ,且与矩形
,且与矩形![]() 的外接圆外切,求动圆
的外接圆外切,求动圆![]() 的圆心的轨迹方程.
的圆心的轨迹方程.
18.(本小题共13分)
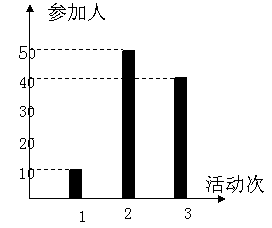 某中学号召学生在今年春节期间至少参加一次社会公益活动(以下简称活动).
某中学号召学生在今年春节期间至少参加一次社会公益活动(以下简称活动).
该校合唱团共有100名学生,他们参加活动的次数统计如图所示.
(I)求合唱团学生参加活动的人均次数;
(II)从合唱团中任意选两名学生,求他们
参加活动次数恰好相等的概率.
(III)从合唱团中任选两名学生,
用![]() 表示这两人参加活动次数之差的绝对值,
表示这两人参加活动次数之差的绝对值,
求随机变量![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
19.(本小题共13分)
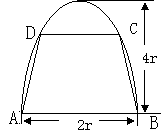 如图,有一块半椭圆形钢板,其半轴长为
如图,有一块半椭圆形钢板,其半轴长为![]() ,短半轴长为
,短半轴长为![]() ,计划将此钢板切割成
,计划将此钢板切割成
等腰梯形的形状,下底![]() 是半椭圆的短轴,上底
是半椭圆的短轴,上底![]() 的端点在椭圆上,
的端点在椭圆上,
记![]() ,梯形面积为
,梯形面积为![]() .
.
(I)求面积![]() 以
以![]() 为自变量的函数式,并写出其定义域;
为自变量的函数式,并写出其定义域;
(II)求面积![]() 的最大值.
的最大值.
20.已知集合![]() ,其中
,其中![]() ,由
,由![]() 中的元素
中的元素
构成两个相应的集合:
![]() ,
,![]() .
.
其中![]() 是有序数对,集合
是有序数对,集合![]() 和
和![]() 中的元素个数分别为
中的元素个数分别为![]() 和
和![]() .
.
若对于任意的![]() ,总有
,总有![]() ,则称集合
,则称集合![]() 具有性质
具有性质![]() .
.
(I)检验集合![]() 与
与![]() 是否具有性质
是否具有性质![]() 并对其中具有性质
并对其中具有性质![]() 的集合,
的集合,
写出相应的集合![]() 和
和![]() ;
;
(II)对任何具有性质![]() 的集合
的集合![]() ,证明:
,证明: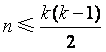 ;
;
(III)判断![]() 和
和![]() 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。