三、解答题
17.(本小题满分12分)
已知函数![]() .
.
(Ⅰ)求函数![]() 的最小正周期;
的最小正周期;
(Ⅱ)求函数![]() 在区间
在区间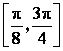 上的最小值和最大值.
上的最小值和最大值.
18.(本小题满分12分)
已知甲盒内有大小相同的1个红球和3个黑球,乙盒内有大小相同的2个红球和
4个黑球.现从甲、乙两个盒内各任取2个球.
(Ⅰ)求取出的4个球均为黑球的概率;
(Ⅱ)求取出的4个球中恰有1个红球的概率;
(Ⅲ)设![]() 为取出的4个球中红球的个数,求
为取出的4个球中红球的个数,求![]() 的分布列和数学期望.
的分布列和数学期望.
19.(本小题满分12分)
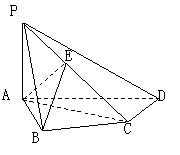
如图,在四棱锥![]() 中,
中,![]() 底面
底面![]() ,
,![]() ,
,
![]() ,
,![]() 是
是![]() 的中点.
的中点.
 (Ⅰ)证明
(Ⅰ)证明![]() ;
;
(Ⅱ)证明![]() 平面
平面![]() ;
;
(Ⅲ)求二面角![]() 的大小.
的大小.
20.(本小题满分12分)
已知函数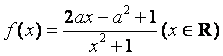 ,其中
,其中![]() .
.
(Ⅰ)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(Ⅱ)当![]() 时,求函数
时,求函数![]() 的单调区间与极值.
的单调区间与极值.
21.(本小题满分14分)
在数列![]() 中,
中,![]() ,其中
,其中![]() .
.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(Ⅲ)证明存在![]() ,使得
,使得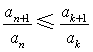 对任意
对任意![]() 均成立.
均成立.
22.(本小题满分14分)
设椭圆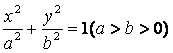 的左、右焦点分别为
的左、右焦点分别为![]() 是椭圆上的一点,
是椭圆上的一点,![]() ,
,
原点![]() 到直线
到直线![]() 的距离为
的距离为![]() .
.
(Ⅰ)证明![]() ;
;
(Ⅱ)设![]() 为椭圆上的两个动点,
为椭圆上的两个动点,![]() ,过原点
,过原点![]() 作直线
作直线![]() 的垂线
的垂线![]() ,
,
垂足为![]() ,求点
,求点![]() 的轨迹方程.
的轨迹方程.
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。