三、解答题

（17）（本小题满分12分）已知<<<,

(Ⅰ)求的值.

（Ⅱ）求.

解答

（18）（本小题满分12分）厂家在产品出厂前，需对产品做检验，厂家将一批

产品发给商家时，商家按合同规定也需随机抽取一定数量的产品做检验，以决定

是否接收这批产品.

（Ⅰ）若厂家库房中的每件产品合格的概率为0.8，从中任意取出4件进行检验.

求至少有1件是合格品的概率;

（Ⅱ）若厂家发给商家20件产品，其中有3件不合格，按合同规定该商家从中任

取2件，都进行检验，只有2件都合格时才接收这批产品，否则拒收.求该商家可

能检验出不合格产品数的分布列及期望，并求该商家拒收这批产品的概率.

解答

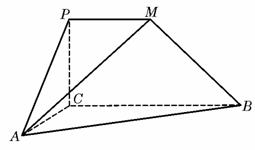
（19）（本小题满分12分）如图，是直角梯形，∠＝90°，∥，

＝1，＝2，又＝1，∠＝120°，⊥，直线与直线所成

的角为60°.

（Ⅰ）求证：平面⊥平面;

（Ⅱ）求二面角的大小;

（Ⅲ）求三棱锥的体积.

解答

（20）（本小题满分12分）设、分别是椭圆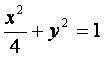的左、右焦点.

（Ⅰ）若是该椭圆上的一个动点，求·的最大值和最小值;

（Ⅱ）设过定点的直线与椭圆交于不同的两点、，且∠为锐角

（其中为坐标原点），求直线的斜率的取值范围.

解答

（21）（本小题满分12分）

已知函数，设曲线在点处的切线与X轴的交点，

其中x₁为正实数。

(Ⅰ)用x_n表示x_n+1；

(Ⅱ)求证：对一切正整数n，的充要条件是；

(Ⅲ)若x₁=4，记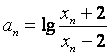，证明数列{an}成等比数列，并求数列{an}的通项公式。

解答

(22)(本小题满分14分)

设函数.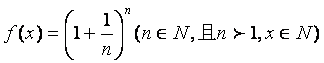

(Ⅰ)当x=6时,求的展开式中二项式系数最大的项;

(Ⅱ)对任意的实数x,证明＞

(Ⅲ)是否存在,使得an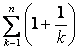＜＜恒成立?若存在,试证明你的结论

并求出a的值;若不存在,请说明理由.

解答