 满足
满足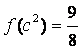 .
.三、解答题
17.(本小题满分12分)
已知函数 满足
满足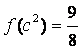 .
.
(1)求常数![]() 的值;
的值;
(2)解不等式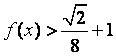 .
.
18.(本小题满分12分)
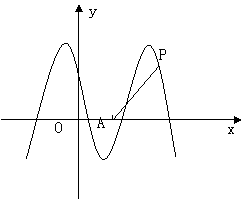 如图,函数
如图,函数![]() 的图象与
的图象与![]() 轴相交于点
轴相交于点![]() ,
,
且该函数的最小正周期为![]() .
.
(1)求![]() 和
和![]() 的值;
的值;
![]()
(2)已知点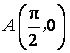 ,点
,点![]() 是该函数图象
是该函数图象
上一点,点![]() 是
是![]() 的中点,
的中点,
当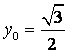 ,
,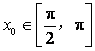 时,求
时,求![]() 的值.
的值.
19.(本小题满分12分)
栽培甲、乙两种果树,先要培育成苗,然后再进行移栽.已知甲、乙两种果树
成苗的概率分别为![]() ,
,![]() ,移栽后成活的概率分别为
,移栽后成活的概率分别为![]() ,
,![]() .
.
(1)求甲、乙两种果树至少有一种果树成苗的概率;
(2)求恰好有一种果树能培育成苗且移栽成活的概率.
20.(本小题满分12分)
 右图是一个直三棱柱(以
右图是一个直三棱柱(以![]() 为底面)被一平面所截得到的几何体,截面为
为底面)被一平面所截得到的几何体,截面为![]() .
.
已知![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)设点![]() 是
是![]() 的中点,证明:
的中点,证明:![]() 平面
平面![]() ;
;
(2)求![]() 与平面
与平面![]() 所成的角的大小;
所成的角的大小;
(3)求此几何体的体积.
21.(本小题满分12分)
设![]() 为等比数列,
为等比数列,![]() ,
,![]() .
.
(1)求最小的自然数![]() ,使
,使![]() ;
;
(2)求和: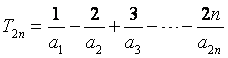 .
.
22.(本小题满分14分)
设动点![]() 到点
到点![]() 和
和![]() 的距离分别为
的距离分别为![]() 和
和![]() ,
,![]() ,
,
且存在常数![]() ,使得
,使得![]() .
.
 (1)证明:动点
(1)证明:动点![]() 的轨迹
的轨迹![]() 为双曲线,并求出
为双曲线,并求出![]() 的方程;
的方程;
(2)如图,过点![]() 的直线与双曲线
的直线与双曲线![]() 的右支交于
的右支交于![]() 两点.
两点.
问:是否存在![]() ,使
,使![]() 是以点
是以点![]() 为直角顶点的等腰
为直角顶点的等腰
直角三角形?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.