 在区间
在区间三、解答题
17.(本小题满分12分)
已知函数 在区间
在区间![]() 内连续,且
内连续,且![]() .
.
(1)求实数![]() 和
和![]() 的值;
的值;
(2)解不等式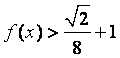 .
.
18.(本小题满分12分)
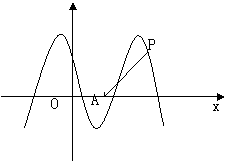 如图,函数
如图,函数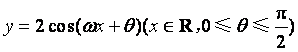 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,
,
且在该点处切线的斜率为![]() .
.
(1)求![]() 和
和![]() 的值;
的值;
![]()
(2)已知点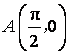 ,点
,点![]() 是该函数图象上一点,
是该函数图象上一点,
点![]() 是
是![]() 的中点,当
的中点,当 ,
,![]() 时,求
时,求![]() 的值.
的值.
19.(本小题满分12分)
某陶瓷厂准备烧制甲、乙、丙三件不同的工艺品,制作过程必须先后经过两次
烧制,当第一次烧制合格后方可进入第二次烧制,两次烧制过程相互独立.根
据该厂现有的技术水平,经过第一次烧制后,甲、乙、丙三件产品合格的概率
依次为![]() ,
,![]() ,
,![]() ,经过第二次烧制后,甲、乙、丙三件产品合格的概率依
,经过第二次烧制后,甲、乙、丙三件产品合格的概率依
次为![]() ,
,![]() ,
,![]() .
.
(1)求第一次烧制后恰有一件产品合格的概率;
(2)经过前后两次烧制后,合格工艺品的个数为![]() ,求随机变量
,求随机变量![]() 的期望.
的期望.
20.(本小题满分12分)
 右图是一个直三棱柱(以
右图是一个直三棱柱(以![]() 为底面)被一平面所截得到的几何体,截面为
为底面)被一平面所截得到的几何体,截面为![]() .
.
已知![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)设点![]() 是
是![]() 的中点,证明:
的中点,证明:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的大小;
的大小;
(3)求此几何体的体积.
21.(本小题满分12分)
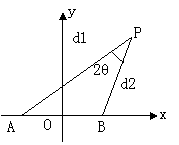 设动点
设动点![]() 到点
到点![]() 和
和![]() 的距离分别为
的距离分别为![]() 和
和![]() ,
,![]() ,且存在常数
,且存在常数![]() ,
,
使得![]() .
.
(1)证明:动点![]() 的轨迹
的轨迹![]() 为双曲线,并求出
为双曲线,并求出![]() 的方程;
的方程;
(2)过点![]() 作直线双曲线
作直线双曲线![]() 的右支于
的右支于![]() 两点,
两点,
试确定![]() 的范围,使
的范围,使![]() ,其中点
,其中点![]() 为坐标原点.
为坐标原点.
22.(本小题满分14分)
设正整数数列![]() 满足:
满足:![]() ,且对于任何
,且对于任何![]() ,有
,有 .
.
(1)求![]() ,
,![]() ;
;
(3)求数列![]() 的通项
的通项![]() .
.
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。