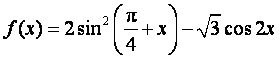 ,
,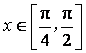 .
.三、解答题
16.(本小题满分12分)
已知函数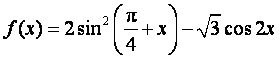 ,
,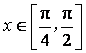 .
.
(I)求![]() 的最大值和最小值;
的最大值和最小值;
(II)若不等式![]() 在
在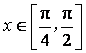 上恒成立,求实数
上恒成立,求实数![]() 的取值范围.
的取值范围.
17.(本小题满分12分)
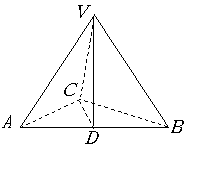 如图,在三棱锥
如图,在三棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,且
的中点,且![]() ,
,
![]() .
.
(I)求证:平面![]() 平面
平面![]() ;
;
(II)试确定角![]() 的值,使得直线
的值,使得直线![]() 与
与
平面![]() 所成的角为
所成的角为![]() .
.
18.(本小题满分12分)
某商品每件成本9元,售价为30元,每星期卖出432件,如果降低价格,销售量
可以增加,且每星期多卖出的商品件数与商品单价的降低值![]()
(单位:元,![]() )的平方成正比,已知商品单价降低2元时,
)的平方成正比,已知商品单价降低2元时,
一星期多卖出24件.
(I)将一个星期的商品销售利润表示成![]() 的函数;
的函数;
(II)如何定价才能使一个星期的商品销售利润最大?
19.(本小题满分12分)
设二次函数![]() ,方程
,方程![]() 的两根
的两根![]() 和
和![]() 满足
满足![]() .
.
(I)求实数![]() 的取值范围;
的取值范围;
(II)试比较![]() 与
与![]() 的大小.并说明理由.
的大小.并说明理由.
20.(本小题满分13分)
已知数列![]() 和
和![]() 满足:
满足:![]() ,
,![]() ,
,![]() ,
,![]() (
(![]() ),
),
且![]() 是以
是以![]() 为公比的等比数列.
为公比的等比数列.
(I)证明:![]() ;
;
(II)若![]() ,证明数列
,证明数列![]() 是等比数列;
是等比数列;
(III)求和: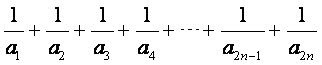 .
.
21.(本小题满分14分)
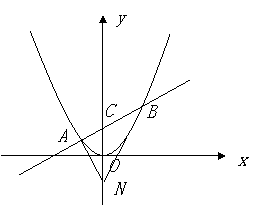
在平面直角坐标系![]() 中,过定点
中,过定点![]() 作直线与抛物线
作直线与抛物线![]() (
(![]() )
)
相交于![]() 两点.
两点.
(I)若点![]() 是点
是点![]() 关于坐标原点
关于坐标原点![]() 的对称点,求
的对称点,求![]() 面积的最小值;
面积的最小值;
(II)是否存在垂直于![]() 轴的直线
轴的直线![]() ,使得
,使得![]() 被以
被以![]() 为直径的圆截得的
为直径的圆截得的
弦长恒为定值?若存在,求出![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
(此题不要求在答题卡上画图)
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。