解答题
全国卷Ⅰ(理)
(17)(本小题满分10分)
设锐角三角形![]() 的内角
的内角![]() 的对边分别为
的对边分别为![]() ,
,![]() .
.
(Ⅰ)求![]() 的大小;
的大小;
(Ⅱ)求![]() 的取值范围.
的取值范围.
全国卷Ⅱ(理)
17.(本小题满分10分)
在![]() 中,已知内角
中,已知内角![]() ,边
,边![]() .设内角
.设内角![]() ,周长为
,周长为![]() .
.
(1)求函数![]() 的解析式和定义域;
的解析式和定义域;
(2)求![]() 的最大值.
的最大值.
北京卷(理)
15.(本小题共13分)
数列![]() 中,
中,![]() ,
,![]() (
(![]() 是常数,
是常数,![]() ),
),
且![]() 成公比不为
成公比不为![]() 的等比数列.
的等比数列.
(I)求![]() 的值;
的值;
(II)求![]() 的通项公式.
的通项公式.
天津卷(理)
17.(本小题满分12分)
已知函数![]() .
.
(Ⅰ)求函数![]() 的最小正周期;
的最小正周期;
(Ⅱ)求函数![]() 在区间
在区间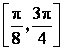 上的最小值和最大值.
上的最小值和最大值.
上海卷(理)
16.(本题满分12分)
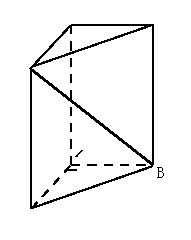 如图,在体积为1的直三棱柱
如图,在体积为1的直三棱柱![]() 中,
中,
![]() .
.
求直线![]() 与平面
与平面![]() 所成角的大小
所成角的大小
(结果用反三角函数值表示).
辽宁卷(理)
17.(本小题满分12分)
已知函数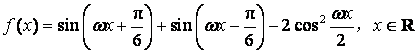 (其中
(其中![]() )
)
(I)求函数![]() 的值域;
的值域;
(II)若对任意的![]() ,函数
,函数![]() ,
,![]() 的图象与直线
的图象与直线![]() 有且仅有两个
有且仅有两个
不同的交点,试确定![]() 的值(不必证明),并求函数
的值(不必证明),并求函数![]() 的单调增区间.
的单调增区间.
江苏卷
17.(本题满分12分)
某气象站天气预报的准确率为![]() ,计算(结果保留到小数点后第2位):
,计算(结果保留到小数点后第2位):
(1)5次预报中恰有2次准确的概率;(4分)
(2)5次预报中至少有2次准确的概率;(4分)
(3)5次预报中恰有2次准确,且其中第3次预报准确的概率.(4分)
浙江卷(理)
(18)(本题14分)已知![]() 的周长为
的周长为![]() ,且
,且![]() .
.
(I)求边![]() 的长;
的长;
(II)若![]() 的面积为
的面积为![]() ,求角
,求角![]() 的度数.
的度数.
福建卷(理)
17.(本小题满分12分)
在![]() 中,
中,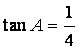 ,
,![]() .
.
(Ⅰ)求角![]() 的大小;
的大小;
(Ⅱ)若![]() 最大边的边长为
最大边的边长为![]() ,求最小边的边长.
,求最小边的边长.
湖北卷(理)
16.(本小题满分12分)
已知![]() 的面积为
的面积为![]() ,且满足
,且满足![]() ,设
,设![]() 和
和![]() 的夹角为
的夹角为![]() .
.
(I)求![]() 的取值范围;
的取值范围;
(II)求函数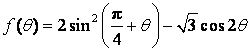 的最大值与最小值.
的最大值与最小值.
湖南卷(理)
16.(本小题满分12分)
已知函数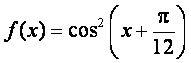 ,
,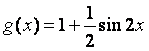 .
.
(I)设![]() 是函数
是函数![]() 图象的一条对称轴,求
图象的一条对称轴,求![]() 的值.
的值.
(II)求函数![]() 的单调递增区间.
的单调递增区间.
广东卷(理)
16.(本小题满分12分)
已知![]() 顶点的直角坐标分别为
顶点的直角坐标分别为![]() ,
,![]() ,
,![]() .
.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若![]() 是钝角,求
是钝角,求![]() 的取值范围.
的取值范围.
重庆卷(理)
17.(本小题满分13分,其中(Ⅰ)小问9分,(Ⅱ)小问4分.)
设![]() .
.
(Ⅰ)求![]() 的最大值及最小正周期;
的最大值及最小正周期;
(Ⅱ)若锐角![]() 满足
满足![]() ,求
,求![]() 的值.
的值.
山东卷(理)
(17)(本小题满分12分)
设数列![]() 满足
满足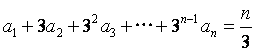 ,
,![]() .
.
(Ⅰ)求数列![]() 的通项;
的通项;
(Ⅱ)设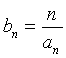 ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() .
.
江西卷(理)
17.(本小题满分12分)
已知函数 在区间
在区间![]() 内连续,且
内连续,且![]() .
.
(1)求实数![]() 和
和![]() 的值;
的值;
(2)解不等式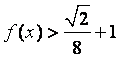 .
.
陕西卷(理)
17.(本小题满分12分)
设函数![]() ,其中向量
,其中向量![]() ,
,![]() ,
,![]() ,
,
且![]() 的图象经过点
的图象经过点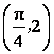 .
.
(Ⅰ)求实数![]() 的值;
的值;
(Ⅱ)求函数![]() 的最小值及此时
的最小值及此时![]() 值的集合.
值的集合.
四川卷(理)
(17)(本小题满分12分)已知![]() <
<![]() <
<![]() <
<![]() ,
,
(Ⅰ)求![]() 的值.
的值.
(Ⅱ)求![]() .
.
安徽卷(理)
16.(本小题满分12分)
已知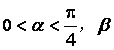 为
为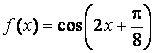 的最小正周期,
的最小正周期,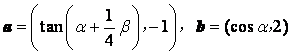 ,
,
且![]()
![]() .求
.求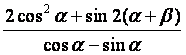 的值.
的值.
海南宁夏卷(理)
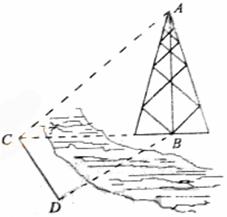
17.(本小题满分12分)
如图,测量河对岸的塔高![]() 时,可以选与塔底
时,可以选与塔底![]() 在同一水平面内的两个测点
在同一水平面内的两个测点![]() 与
与![]() .
.
现测得![]() ,并在点
,并在点![]() 测得塔顶
测得塔顶![]() 的仰角为
的仰角为![]() ,求塔高
,求塔高![]() .
.
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。