三、解答题
15.(本小题共13分)
数列![]() 中,
中,![]() ,
,![]() (
(![]() 是常数,
是常数,![]() ),
),
且![]() 成公比不为
成公比不为![]() 的等比数列.
的等比数列.
 (I)求
(I)求![]() 的值;
的值;
(II)求![]() 的通项公式.
的通项公式.
16.(本小题共14分)
如图,在![]() 中,
中,![]() ,斜边
,斜边![]() .
.![]() 可以通过
可以通过![]() 以
以
直线![]() 为轴旋转得到,且二面角
为轴旋转得到,且二面角![]() 是直二面角.动点
是直二面角.动点![]() 的斜边
的斜边![]() 上.
上.
(I)求证:平面![]() 平面
平面![]() ;
;
(II)当![]() 为
为![]() 的中点时,求异面直线
的中点时,求异面直线![]() 与
与![]() 所成角的大小;
所成角的大小;
(III)求![]() 与平面
与平面![]() 所成角的最大值.
所成角的最大值.
17.(本小题共14分)
矩形![]() 的两条对角线相交于点
的两条对角线相交于点![]() ,
,![]() 边所在直线的方程为
边所在直线的方程为![]() ,
,
点![]() 在
在![]() 边所在直线上.
边所在直线上.
(I)求![]() 边所在直线的方程;
边所在直线的方程;
(II)求矩形![]() 外接圆的方程;
外接圆的方程;
(III)若动圆![]() 过点
过点![]() ,且与矩形
,且与矩形![]() 的外接圆外切,求动圆
的外接圆外切,求动圆![]() 的圆心的轨迹方程.
的圆心的轨迹方程.
18.(本小题共13分)
 某中学号召学生在今年春节期间至少参加一次社会公益活动(以下简称活动).
某中学号召学生在今年春节期间至少参加一次社会公益活动(以下简称活动).
该校合唱团共有100名学生,他们参加活动的次数统计如图所示.
(I)求合唱团学生参加活动的人均次数;
(II)从合唱团中任意选两名学生,求他们
参加活动次数恰好相等的概率.
(III)从合唱团中任选两名学生,
用![]() 表示这两人参加活动次数之差的绝对值,
表示这两人参加活动次数之差的绝对值,
求随机变量![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
19.(本小题共13分)
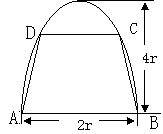 如图,有一块半椭圆形钢板,其半轴长为
如图,有一块半椭圆形钢板,其半轴长为![]() ,短半轴长为
,短半轴长为![]() ,计划将此钢板切割成
,计划将此钢板切割成
等腰梯形的形状,下底![]() 是半椭圆的短轴,上底
是半椭圆的短轴,上底![]() 的端点在椭圆上,
的端点在椭圆上,
记![]() ,梯形面积为
,梯形面积为![]() .
.
(I)求面积![]() 以
以![]() 为自变量的函数式,并写出其定义域;
为自变量的函数式,并写出其定义域;
(II)求面积![]() 的最大值.
的最大值.
20.已知集合![]() ,其中
,其中![]() ,由
,由![]() 中的元素
中的元素
构成两个相应的集合:
![]() ,
,![]() .
.
其中![]() 是有序数对,集合
是有序数对,集合![]() 和
和![]() 中的元素个数分别为
中的元素个数分别为![]() 和
和![]() .
.
若对于任意的![]() ,总有
,总有![]() ,则称集合
,则称集合![]() 具有性质
具有性质![]() .
.
(I)检验集合![]() 与
与![]() 是否具有性质
是否具有性质![]() 并对其中具有性质
并对其中具有性质![]() 的集合,
的集合,
写出相应的集合![]() 和
和![]() ;
;
(II)对任何具有性质![]() 的集合
的集合![]() ,证明:
,证明: ;
;
(III)判断![]() 和
和![]() 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。