解答题
(17)(本大题满分12分)
数列![]() 的前
的前![]() 项和记为
项和记为![]()
(Ⅰ)求![]() 的通项公式;
的通项公式;
(Ⅱ)等差数列![]() 的各项为正,其前
的各项为正,其前![]() 项和为
项和为![]() ,且
,且![]() ,
,
又![]() 成等比数列,求
成等比数列,求![]()
(18)(本大题满分12分)
已知![]() 是三角形
是三角形![]() 三内角,向量m=(-1,
三内角,向量m=(-1,![]() ),n=(cosA,sinA),且mn=1.
),n=(cosA,sinA),且mn=1.
(Ⅰ)求角![]() ;
;
(Ⅱ)若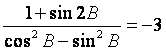 ,求tanC.
,求tanC.
(19)(本大题满分12分)
某课程考核分理论与实验两部分进行,每部分考核成绩只记“合格”与
“不合格”,两部分考核都是“合格”则该课程考核“合格”,甲、乙、
丙三人在理论考核中合格的概率分别为![]() ;在实验考核中合格的概
;在实验考核中合格的概
率分别为![]() ,所有考核是否合格相互之间没有影响
,所有考核是否合格相互之间没有影响
(Ⅰ)求甲、乙、丙三人在理论考核中至少有两人合格的概率;
(Ⅱ)求这三人该课程考核都合格的概率。(结果保留三位小数)
(20)(本大题满分12分)
如图,在长方体![]() 中,
中,![]() 分别是
分别是![]() 的中点,
的中点,
![]() 分别是
分别是![]() 的中点,
的中点,![]()
(Ⅰ)求证:![]() 面
面![]() ;
;
(Ⅱ)求二面角![]() 的大小。
的大小。
(21)(本大题满分12分)
已知函数![]() ,其中
,其中![]() 是
是![]() 的导函数
的导函数
(Ⅰ)对满足![]() 的一切
的一切![]() 的值,都有
的值,都有![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)设![]() ,当实数
,当实数![]() 在什么范围内变化时,函数
在什么范围内变化时,函数![]() 的图象与
的图象与
直线![]() 只有一个公共点
只有一个公共点
(22)(本大题满分14分)
已知两定点![]() ,满足条件
,满足条件![]() 的点
的点![]() 的轨迹是
的轨迹是
曲线![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点
两点
(Ⅰ)求![]() 的取值范围;
的取值范围;
(Ⅱ)如果![]() ,且曲线
,且曲线![]() 上存在点
上存在点![]() ,使
,使![]() ,
,
求![]() 的值和
的值和![]() 的面积S.
的面积S.