成立的x的取值集合。解答题
16.（本小题满分12分）
设向量a=（sinx，cos x），b=（cosx，cosx），x∈R，函数f（x）=a（a+b）。
（Ⅰ）求函数f（x）的最大值与最小正周期；
（Ⅱ）求使不等式f（x）≥成立的x的取值集合。
17．（本小题满分12分）
某单位最近组织了一次健身活动，活动分为登山组和游泳组，且每个职工至多参
加了其中一组，在参加活动的职工中，青年人占42.5%，中年人占47.5%，老年人
占10%。登山组的职工占参加活动总人数的
，且该组中，青年人占50%，中年人
占40%，老年人占10%。为了了解各组不同年龄层次的职工对本次活动的满意程度，
现用分层抽样方法从参加活动的全体职工中抽取一个容量为200的样本，试确定
（Ⅰ）游泳组中，青年人、中年人、老年人分别所占的比例；
（Ⅱ）游泳组中，青年人、中年人、老年人分别应抽取的人数。
18．（本小题满分12分）
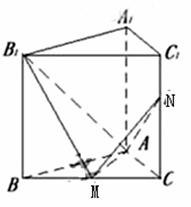
如图，已知正三棱柱ABC—A1B1C1的侧棱长和底面边长为1，M是底面BC边上的中点，
N是侧棱CC1上的点，且CN=2C1N。
（Ⅰ）求二面角B1—AM—N的平面角的余弦值；
（Ⅱ）求点B1到平面AMN的距离。
19．（本小题满分12分）
设函数f（x）=x3-ax2+bx+c在x=1处取得极值-2，试用c表示a和b，并求f（x）
的单调区间。
20（本小题满分13分）
设数列{an}的前n项和为Sn，点（n，
）（n∈N*）均在函数y=3x-2的图像上。
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）设bn=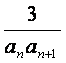
，Tn是数列{bn}的前n项和，求使得Tn＜
对所有n∈N*都成立的最小正整数m。
21．（本小题满分14分）
设A、B分别为椭圆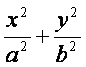
=1（a，b＞0）的左、右顶点，椭圆长半轴的长等于焦距，
且x=4是它的右准线。
（Ⅰ）求椭圆的方程；
（Ⅱ）设P为右准线上不同于点（4，0）的任意一点，若直线AB，BP分别与椭圆相交于
异于A，B的M、N，证明点B在以MN为直径的圆内.
本课件完全公益，使用过程中有任何问题，或想参与新课件制作，请加开心教练QQ：29443574。