解答题

 全国卷Ⅰ(文)

(20) (本小题满分12分)

如图，l、l是互相垂直的异面直线，MN是它们的公垂线段.点A、B在上l，

C在l上,AM=MB=MN.

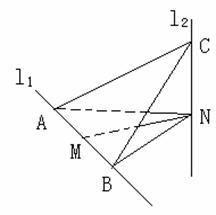
（Ⅰ）证明AC；

（Ⅱ）若，求NB与平面ABC所成角的余弦值.

解答

全国卷Ⅱ(文)

（20）（本小题１２分）

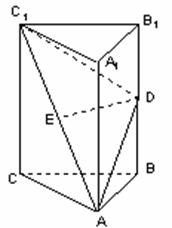
 如图，在直三棱柱中，、分别为、的中点。

（I）证明：ED为异面直线与的公垂线；

（II）设求二面角的大小

  解答

北京卷(文)

(18)(本小题共13分)

    某公司招聘员工，指定三门考试课程，有两种考试方案．

    方案一：考试三门课程，至少有两门及格为考试通过：

    方案二：在三门课程中，随机选取两门，这两门都及格为考试通过．

    假设某应聘者对三门指定课程考试及格的概率分别是0．5，0．6，0．9，

且三门课程考试是否及格相互之间没有影响．求：

(Ⅰ)该应聘者用方案一考试通过的概率；

(Ⅱ)该应聘者用方案二考试通过的概率．

解答

天津卷(文)

(20)(本小题满分12分)

    已知函数f(x)=4x³-3x²cosθ+，其中x∈R，θ为参数，且0≤θ≤.

    (Ⅰ)当cosθ=0时，判断函数f(x)是否有极值；

    (Ⅱ)要使函数f(x)的极小值大于零，求参数θ的取值范围；

    (Ⅲ)若对(Ⅱ)中所求的取值范围内的任意参数θ，函数f(x)在区间(2a-1，a)

内都是增函数，求实数a的取值范围.

 解答

上海卷(文)

20(本题满分14分)本题共有2个小题，第1小题满分7分，第2小题满分7分.

设数列{a_n}的前n项和为S_n，且对任意正整数n，a_n+S_n=4096.

(1)求数列{a_n}的通项公式：

(2)设数列{log₂a_n}的前n项和为T_n.对数列{T_n}，从第几项起T_n＜-509？

解答

辽宁卷(文)

20．（本小题满分12分）

已知等差数列的前项和为，．

（1）求的值；

（2）若与的等差中项为，满足，求数列的前项和．

 解答

     江苏卷

（20）（本小题满分16分，第一小问4分，第二小问满分6分，第三小问满分6分）

　　　设a为实数，设函数的最大值为g(a)。

　　　（Ⅰ）设t＝，求t的取值范围，并把f(x)表示为t的函数m(t)

（Ⅱ）求g(a)

（Ⅲ）试求满足的所有实数a

解答

浙江卷(文)

(18)甲、乙两袋装有大小相同的红球和白球，甲袋装有2个红球，2个白球；

乙袋装有2个红球，n个白球．现从甲、乙两袋中各任取2个球．

    (Ⅰ)若n=3，求取到的4个球全是红球的概率；

    (Ⅱ)若取到的4个球中至少有2个红球的概率为，求n．

解答

福建卷(文)

（20）（本小题满分12分）

       已知椭圆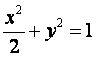的左焦点为F，O为坐标原点。

       （I）求过点O、F，并且与椭圆的左准线相切的圆的方程；

       （II）设过点F的直线交椭圆于A、B两点，并且线段AB的

              中点在直线上，求直线AB的方程。

      解答

湖北卷(文)

19．（本小题满分12分）

设函数f（x）=x³-ax²+bx+c在x=1处取得极值-2，试用c表示a和b，并求f（x）

的单调区间。

解答

湖南卷(文)

19．(本小题满分14分)

    已知函数f(x)=ax³-3x²+1-.

    (Ⅰ)讨论函数f(x)的单调性；

    (Ⅱ)若曲线y=f(x)上两点A、B处的切线都与y轴垂直，且线段AB与x轴有公共点，

求实数a的取值范围.

解答

广东卷

18．（本小题满分14分）

    设函数f(x)=-x³+3x+2分别在x₁、x₂处取得极小值、极大值。xoy平面

上点A、B的坐标分别为（x₁，f(x₁)）、（x₂，f(x₂)）。该平面上动点P满

足，点Q是点P关于直线y=2(x-4)的对称点，求：

（Ⅰ）点A、B的坐标：

（Ⅱ）动点Q的轨迹方程。

解答

重庆卷(文)

(20)（本小题满分12分）

如图，在正四棱柱ABCD-A₁B₁C₁D₁中：AB=1，BB₁=+1，E为BB₁上

使B₁E=1的点，平面AEC₁交DD₁于F，交A₁D₁的延长线于G.求：

（Ⅰ）异面直线AD与C₁G所成的角的大小；

（Ⅱ）二面角A-C₁G-A₁的正切值.

        解答

山东卷(文)

(20) （本小题满分12分）

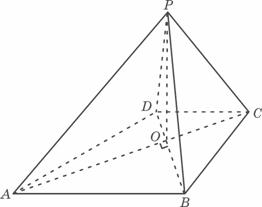如图，已知四棱锥P-ABCD的底面ABCD为等腰梯形，AB∥CD,AC⊥BD,AC与BD

相交于点O，且顶点P在底面上的射影恰为O点，又BO=2,PO=,PB⊥PD.

(Ⅰ)求异面直线PD与BC所成角的余弦值；

(Ⅱ)求二面角P-AB-C的大小；

(Ⅲ)设点M在棱PC上，且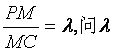为何值时，PC⊥平面BMD.

解答

江西卷(文)

20．(本小题满分12分)

如图，已知三棱锥O-ABC的侧棱OA、OB、OC两两垂直，且OA=1，OB=OC=2，

E是OC的中点．

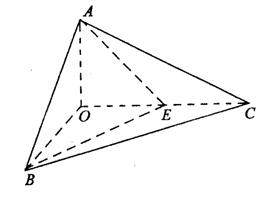
    (1)求O点到面ABC的距离；

    (2)求异面直线BE与AC所成的角；

    (3)求二面角E-AB-C的大小．

解答

 陕西卷(文)

20．（本小题满分12分）

已知正项数列，其前n项和S_n满足10S_n=＋5a_n＋6，

且a₁，a₃，a₁₅成等比数列，求数列的通项a_n.

解答

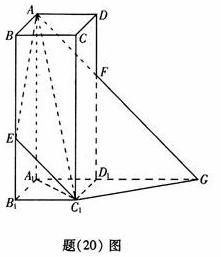
 四川卷(文)

（20）（本大题满分12分）

如图，在长方体中，分别是的中点，

分别是的中点，

（Ⅰ）求证：面；

（Ⅱ）求二面角的大小。

解答

 安徽卷(文)

（20）（本大题满分12分）设函数，已知

是奇函数。

（Ⅰ）求、的值。

（Ⅱ）求的单调区间与极值。

     解答