 .
.解答题
全国卷Ⅰ(理)
(21)(本小题满分14分)
已知函数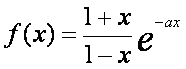 .
.
(Ⅰ)设![]() 讨论
讨论![]() 的单调性;
的单调性;
(Ⅱ)若对任意![]() 恒有
恒有![]() ,求a的取值范围。
,求a的取值范围。
全国卷Ⅱ(理)
(21)(本小题满分为14分)
已知抛物线![]() 的焦点为F,A、B是热线上的两动点,且
的焦点为F,A、B是热线上的两动点,且![]()
过A、B两点分别作抛物线的切线,设其交点为M。
(I)证明![]() 为定值;
为定值;
(II)设![]() 的面积为S,写出
的面积为S,写出![]() 的表达式,并求S的最小值。
的表达式,并求S的最小值。
北京卷(理)
(19)(本小题共14分)
已知点M(-2,0),N(2,0),动点P满足条件|PM|-|PN|=2![]() .记动点P的
.记动点P的
轨迹为W.
(Ⅰ)求W的方程;
(Ⅱ)若A,B是W上的不同两点,O是坐标原点,求![]() 的最小值.
的最小值.
天津卷(理)
(21)(本小题满分14分)
已知数列{xn}、{yn}满足x1=x2=1,y1=y2=2,并且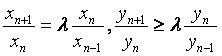
(![]() 为非零参数,n=2,3,4,…).
为非零参数,n=2,3,4,…).
(Ⅰ)若x1、x3、x5成等比数列,求参数![]() 的值;
的值;
(Ⅱ)当![]() >0时,证明
>0时,证明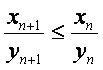 (n∈N*);
(n∈N*);
(Ⅲ)当![]() >1时,证明
>1时,证明 <
<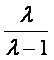 (n∈N*).
(n∈N*).
上海卷(理)
21.(本题满分16分)本题共有3个小题,第1小题满分4分,第2小题满分6分,
第3小题满分6分)
已知有穷数列![]()
![]()
![]() 共有2
共有2![]() 项(整数
项(整数![]() ≥2),首项
≥2),首项![]() =2.设该数列的前
=2.设该数列的前![]() 项
项
和为![]() ,且
,且![]() =
=![]() +2(
+2(![]() =1,2,┅,2
=1,2,┅,2![]() -1),其中常数
-1),其中常数![]() >1.
>1.
(1)求证:数列![]()
![]()
![]() 是等比数列;
是等比数列;
(2)若![]() =2
=2![]() ,数列
,数列![]()
![]()
![]() 满足
满足![]() =
=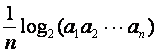 (
(![]() =1,2,┅,2
=1,2,┅,2![]() ),
),
求数列![]()
![]()
![]() 的通项公式;
的通项公式;
(3)若(2)中的数列![]()
![]()
![]() 满足不等式
满足不等式
|![]() -
-![]() |+|
|+|![]() -
-![]() |+┅+|
|+┅+|![]() -
-![]() |+|
|+|![]() -
-![]() |≤4,求
|≤4,求![]() 的值.
的值.
辽宁卷
21.(本小题满分12分)
已知函数f(x)=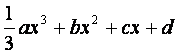 ,其中a
, b , c是以d为公差的等差数列,,
,其中a
, b , c是以d为公差的等差数列,,
且a>0,
d>0.设![]() [1-
[1-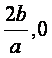 ]上,
]上,![]() 在
在![]() 处取得
处取得
最大值,在![]() ,将点
,将点![]() 依次记为A,
依次记为A,
B,
C.![]()
(I)求![]()
(II)若⊿ABC有一边平行于x轴,且面积为![]() ,求a
,d的值
,求a
,d的值
江苏卷
(21)(本小题满分14分)
设数列![]() 、
、![]() 、
、![]() 满足:
满足:![]() ,
,![]() (n=1,2,3,…),
(n=1,2,3,…),
证明![]() 为等差数列的充分必要条件是
为等差数列的充分必要条件是![]() 为等差数列且
为等差数列且![]() (n=1,2,3,…)
(n=1,2,3,…)
浙江卷(理)
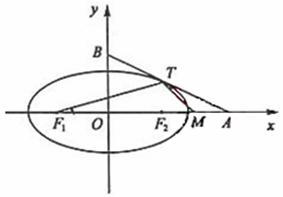
(19)如图,椭圆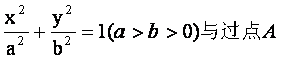 (2,0)、B(0,1)
(2,0)、B(0,1)
的直线有且只有一个公共点T,且椭圆的离心率e=![]() 。
。
(Ⅰ)求椭圆方程;
(Ⅱ)设F1、F2分别为椭圆的左、右焦点,M为线段AF2的中点,
求证:∠ATM=∠AF1T。
福建卷(理)
(21)(本小题满分12分)
已知函数![]()
(I)求![]() 在区间
在区间![]() 上的最大值
上的最大值![]()
(II)是否存在实数![]() 使得
使得![]() 的图象与
的图象与![]() 的图象有且只有三
的图象有且只有三
个不同的交点?若存在,求出![]() 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。
湖北卷(理)
20.(本小题满分14分)
设A、B分别为椭圆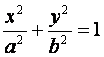 (a,b>0)的左、右顶点,椭圆长半轴的长等于焦距,
(a,b>0)的左、右顶点,椭圆长半轴的长等于焦距,
且x=4为它的右准线。
(Ⅰ)求椭圆的方程;
(Ⅱ)设P为右准线上不同于点(4,0)的任意一点,若直线AP、BP分别与椭圆相交于
异于A、B的点M、N,证明点B在以MN为直径的圆内。
(此题不要求在答题卡上画图)
湖南卷(理)
20.(本小题满分14分)
对1个单位质量的含污物体进行清洗,清洗前其清洁度(含污物体的清洁度定义为:
1-![]() )为0.8,要求洗完后的清洁度是0.99.有两种方案可供选择,方案
)为0.8,要求洗完后的清洁度是0.99.有两种方案可供选择,方案
甲:一次清洗;方案乙:分两次清洗.该物体初次清洗后受残留水等因素影响,其
质量变为a(1≤a≤3).设用x单位质量的水初次清洗后的清洁度是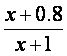 (x>a-1),用
(x>a-1),用
y单位质量的水第二次清洗后的清洁度是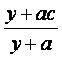 ,其中c(0.8<c<0.99)是该物体初次清
,其中c(0.8<c<0.99)是该物体初次清
洗后的清洁度.
(Ⅰ)分别求出方案甲以及c=0.95时方案乙的用水量,并比较哪一种方案用水量较少;
(Ⅱ)若采用方案乙,当a为某定值时,如何安排初次与第二次清洗的用水量,使总用水
量最少?并讨论a取不同数值时对最少总用水量多少的影响.
广东卷
19.(本小题满分14分)
已知公比为q(0<q<1)的无穷等比数列{an}各项的和为9,无穷等比
数列{an2}各项的和为![]() 。
。
(Ⅰ)求数列{an}的首项a1和公比q:
(Ⅱ)对给定的k(k=1,2,…,n),设T{k}是首项为ak,公差为2ak-1的
等差数列,求数列T{2}的前10项之和:
(Ⅲ)设bi为数列![]() 的第i项,sn=b1+b2+…+bn,求sn,并求正整数
的第i项,sn=b1+b2+…+bn,求sn,并求正整数
m(m>1),使得![]()
![]() 存在且不等于零。
存在且不等于零。
(注:无穷等比数列各项的和即当n![]() 时该无穷等比数列前n项和的极限)
时该无穷等比数列前n项和的极限)
重庆卷(理)
(21)(本小题满分12分)
已知定义域为![]() 的函数
的函数![]() 满足
满足![]() 。
。
(Ⅰ)若![]() ,求
,求![]() ;又若
;又若![]() ,求
,求![]() ;
;
(Ⅱ)设有且仅有一个实数![]() ,使得
,使得![]() ,求函数
,求函数![]() 的解析表达式;
的解析表达式;
山东卷(理)
21.(本小题满分12分)
双曲线C与椭圆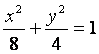 有相同的焦点,直线y=
有相同的焦点,直线y=![]() x为C的一条渐近线.
x为C的一条渐近线.
(Ⅰ)求双曲线C的方程;
(Ⅱ)过点P(0,4)的直线l,交双曲线C于A、B两点,交x轴于Q点
(Q点与C的顶点不重合).当![]() =λ1
=λ1![]() =λ2
=λ2![]() ,且λ1+λ2=
,且λ1+λ2=![]() 时,求Q点的坐标.
时,求Q点的坐标.
江西卷(理)
21.(本小题满分12分)
如图,椭圆Q: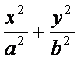 =1(a>b>0)的右焦点为F(c,0),过点F的一动直线m绕
=1(a>b>0)的右焦点为F(c,0),过点F的一动直线m绕
点F转动,并且交椭圆于A、B两点,P为线段AB的中点.
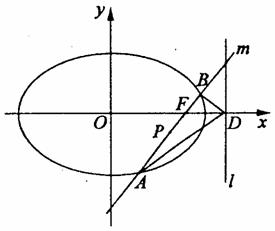
(1)求点P的轨迹H的方程;
(2)若在Q的方程中,令a2=1+cosθ+sinθ,b2=sinθ(0<θ≤![]() ).确定θ的值,使
).确定θ的值,使
原点距椭圆Q的右准线l最远.此时,设l与x轴交点为D,当直线m绕点F转动到
什么位置时,三角形ABD的面积最大?
陕西卷(理)
(21)(本小题满分为12分)
如图,三定点![]() 三动点D、E、M满足
三动点D、E、M满足
![]()
![]()
(I)求动直线DE斜率的变化范围;
(II)求动点M的轨迹方程。
四川卷(理)
(21)(本大题满分12分)
已知函数![]() ,其中
,其中![]() 是
是![]() 的导函数
的导函数
(Ⅰ)对满足![]() 的一切
的一切![]() 的值,都有
的值,都有![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)设![]() ,当实数
,当实数![]() 在什么范围内变化时,函数
在什么范围内变化时,函数![]() 的图象与
的图象与
直线![]() 只有一个公共点
只有一个公共点
安徽卷(理)
(21)(本小题满分12分)
数列![]() 的前n项和为Sn,已知
的前n项和为Sn,已知![]() ,sn=n2an-n(n-1),n=1,2…
,sn=n2an-n(n-1),n=1,2…
(Ⅰ)写出sn与![]() 的递推关系式(n
的递推关系式(n![]() 2),并求sn关于n的表达式:
2),并求sn关于n的表达式:
(Ⅱ)设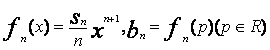 求数列{bn}的前n项和Tn。
求数列{bn}的前n项和Tn。
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。