解答题

 全国卷Ⅰ(理)

（18）（本小题满分12分）

A、B是治疗同一种疾病的两种药，用若干试验组进行对比试验.每个试验组由4只

小白鼠组成，其中2只服用A，另2只服用B，然后观察疗效，若在一个试验组中，

服用A有效的小白鼠的只数比服用B有效的多，就称该试验组为甲类组，设每只小

白鼠服用A有效的概率为，服用B有效的概率为。

（Ⅰ）求一个试验组为甲类组的概率。

（Ⅱ）观察3个试验组，用表示这3个试验组中甲类组的个数，求的分布列和数

学期望。

解答

全国卷Ⅱ(理)

（18）（本小题满分１２分）

某批产品成箱包装，每箱5件，一用户在购进该批产品前先取出3箱，

再从每箱中任意抽取2件产品进行检验。设取出的第一、二、三箱中

分别有0件、1件、2件二等品，其余为一等品。

（I）用表示抽检的6件产品中二等品的件数，求的分布列及的数学期望；

（II）若抽检的6件产品中有2件或2件以上二等品，用户就拒绝购买这批产品，

求这批产品被用户拒绝购买的概率。

解答

北京卷(理)

（16）（本小题共13分）

 已知函数f（x）=ax³+bx²+cx在点x₀处取得极大值5，其导函数y=f′（x）

的图象经过点（1，0），（2，0），如图所示，求：

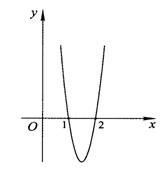
（Ⅰ）x₀的值；

（Ⅱ）a，b，c的值.

^解答

天津卷(理)

(18)(本小题满分12分)

 某射手进行射击训练，假设每次射击击中目标的概率为，

 且各次射击的结果互不影响．

 (Ⅰ)求射手在3次射击中，至少有两次连续击中目标的概率(用数字作答)；

 (Ⅱ)求射手第3次击中目标时，恰好射击了4次的概率(用数字作答)；

 (Ⅲ)设随机变量ξ表示射手第3次击中目标时已射击的次数，求ξ的分布列．

解答

上海卷(理)

18．（本题满分12分）

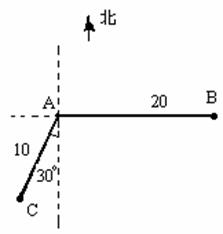
如图，当甲船位于A处时获悉，在其正东方向相距20海里的B处有一艘

渔船遇险等待营救．甲船立即前往救援，同时把消息告知在甲船的南

偏西30，相距10海里C处的乙船，试问乙船应朝北偏东多少度的方向

沿直线前往B处救援（角度精确到1）？

解答

辽宁卷

(18) (本小题满分12分)

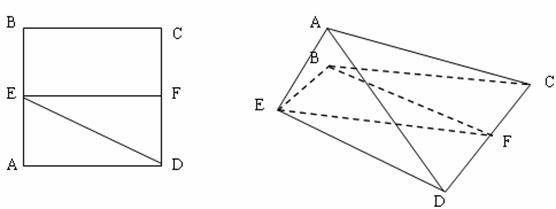
已知正方形.、分别是、的中点,将沿折起,如图

所示,记二面角的大小为.

(I) 证明平面;

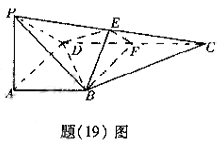
(II)若为正三角形,试判断点在平面内的射影是

否在直线上,证明你的结论,并求角的余弦值.

解答

     江苏卷

（18）（本小题满分14分）

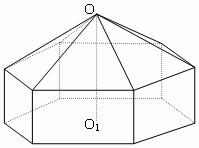
　　　请您设计一个帐篷。它下部的形状是高为1m的正六棱柱，上部的形状是

      侧棱长为3m的正六棱锥（如右图所示）。试问当帐篷的顶点O到底面中

      心的距离为多少时，帐篷的体积最大？

解答

浙江卷(理)

（16）设：

     （Ⅰ）;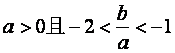

     （Ⅱ）方程在（0，1）内有两个实根。

解答

福建卷(理)

（18）（本小题满分12分）

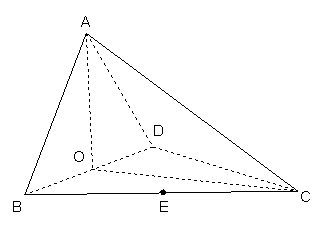
       如图，四面体ABCD中，O、E分别是BD、BC的中点，

       （I）求证：平面BCD；

       （II）求异面直线AB与CD所成角的大小；

       （III）求点E到平面ACD的距离。

 解答

湖北卷(理)

17．（本小题满分13分）

   已知二次函数y=f(x)的图象经过坐标原点，其导函数为.数列{}的

前n项和为S_n，点均在函数y=f(x)的图象上。

  （Ⅰ）求数列{a_n}的通项公式；

  （Ⅱ）设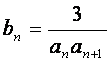，T_n是数列{b_n}的前n项和，求使得T_n＜对所有都成

立的最小正整数m。

   解答

湖南卷(理)

17．(本小题满分12分)

    某安全生产监督部门对5家小型煤矿进行安全检查(简称安检)．若安检不合格，

则必须整改．若整改后经复查仍不合格，则强制关闭．设每家煤矿安检是否合格

是相互独立的，且每家煤矿整改前安检合格的概率是0.5，整改后安检合格的概率

是0.8，计算(结果精确到0.01)：

    (Ⅰ)恰好有两家煤矿必须整改的概率；

    (Ⅱ)平均有多少家煤矿必须整改；

    (Ⅲ)至少关闭一家煤矿的概率．

解答

广东卷

16．（本小题满分12分）

    某运动员射击一次所得环数X的分布如下：

现进行两次射击,以该运动员两次射击中最高环数作为他的成绩,记为。

（Ⅰ）求该运动员两次都命中7环的概率：

（Ⅱ）求的分布列：

（Ⅲ）求的数学期望E。

 解答

重庆卷(理)

（18）（本小题满分13分）

某大厦的一部电梯从底层出发后只能在第18、19、20层可以停靠。若该

电梯在底层载有5位乘客，且每位乘客在这三层的每一层下电梯的概率均

为，用表示这5位乘客在20层下电梯的人数，求：

（Ⅰ）随即变量的分布列；

（Ⅱ）随即变量的期望；

解答

山东卷(理)

18．(本小题满分12分)

    设函数f(x)=ax-(a+1)ln(x+1)，其中a≥-1．求f(x)的单调区间．

解答

江西卷(理)

18．(本小题满分12分)

    某商场举行抽奖促销活动，抽奖规则是：从装有9个白球、1个红球的箱子中每

次随机地摸出一个球，记下颜色后放回，摸出一个红球可获得奖金10元；摸出两个红

球可获得奖金50元．现有甲、乙两位顾客，规定：甲摸一次，乙摸两次．令ξ表示甲、

乙两人摸球后获得的奖金总额．求

   (1)ξ的分布列；           (2)ξ的数学期望．

解答

 陕西卷(理)

（１８）（本小题满分１２分）

甲、乙、丙3人投篮，投进的概率分别是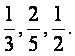

（I）现3人各投篮1次，求3人都没有投进的概率；

（II）用表示投篮3次的进球数，求随机变量的概率分布及数学期望

解答

 四川卷(理)

（18）（本大题满分12分）

已知是三角形三内角，向量m=(-1,),n=(cosA,sinA),且mn=1.

（Ⅰ）求角；

（Ⅱ）若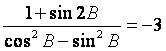，求tanC.

解答

 安徽卷(理)

（18）（本小题满分12分）

在添加剂的搭配适用中，为了找到最佳的搭配方案，需要对各种不同的搭配方式

作比较，在试制某种牙膏新品种时，需要选用两种不同的添加剂。现在芳香度分

别为0，1，2，3，4，5的六种添加剂可供选用。根据实验设计学原理，通常首先

要随机选取两种不同的添加剂进行搭配实验。用表示所选用的两种不同的添加剂

的芳香度之和。

（Ⅰ）写出的分布列：（以列表的形式给出结论，不必写计算过程）

（Ⅱ）求的数学期望E。（要求写出计算过程或说明道理）

解答