三、解答题
(17)(本小题满分13分)
设函数![]() (其中
(其中![]() )。且
)。且![]() 的图像在
的图像在
![]() 轴右侧的第一个最高点的横坐标是
轴右侧的第一个最高点的横坐标是![]() 。
。
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)如果![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() ,求
,求![]() 的值;
的值;
(18)(本小题满分13分)
 某大厦的一部电梯从底层出发后只能在第18、19、20层可以停靠。若该
某大厦的一部电梯从底层出发后只能在第18、19、20层可以停靠。若该
电梯在底层载有5位乘客,且每位乘客在这三层的每一层下电梯的概率均
为![]() ,用
,用![]() 表示这5位乘客在20层下电梯的人数,求:
表示这5位乘客在20层下电梯的人数,求:
(Ⅰ)随即变量![]() 的分布列;
的分布列;
(Ⅱ)随即变量![]() 的期望;
的期望;
(19)(本小题满分13分)
如图,在四棱锥![]() 中,
中,![]() 底面
底面![]() ,
,![]() 为直角,
为直角,![]()
![]() ,
,![]() 、
、![]() 分别为
分别为![]() 、CD的中点。
、CD的中点。
(Ⅰ)试证:![]() 平面
平面![]() ;
;
(Ⅱ)设PA=K·AB,且二面角![]() 的平面角大于
的平面角大于![]() ,求
,求![]() 的取值范围。
的取值范围。

(20)(本小题满分13分)
已知函数![]() ,其中
,其中![]() 为常数。
为常数。
(Ⅰ)若![]() ,讨论函数
,讨论函数![]() 的单调性;
的单调性;
(Ⅱ)若![]() ,且
,且 ,试证:
,试证:![]() ;
;
(21)(本小题满分12分)
已知定义域为![]() 的函数
的函数![]() 满足
满足![]() 。
。
(Ⅰ)若![]() ,求
,求![]() ;又若
;又若![]() ,求
,求![]() ;
;
(Ⅱ)设有且仅有一个实数![]() ,使得
,使得![]() ,求函数
,求函数![]() 的解析表达式;
的解析表达式;
(22)(本小题满分12分)
已知一列椭圆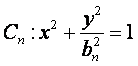 ,
,![]() 若椭圆
若椭圆![]() 上有一点
上有一点![]() ,
,
使![]() 到右准线
到右准线![]() 的距离
的距离![]() 是
是![]() 与
与![]() 的等差中项,
的等差中项,
其中![]() 分别是
分别是![]() 的左、右焦点。
的左、右焦点。
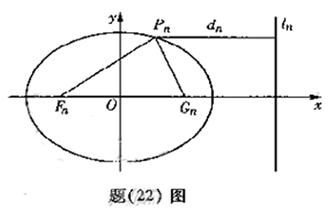
(Ⅰ)试证: ;
;
(Ⅱ)取 ,并用
,并用![]() 表示
表示![]() 的面积,
的面积,
试证:![]() 且
且![]()
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。