解答题
全国卷Ⅰ(理)
(17)(本大题满分12分)
设函数![]() 图像的一条对称轴是直线
图像的一条对称轴是直线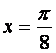
![]()
(Ⅰ)求![]() ;
;
(Ⅱ)求函数![]() 的单调增区间;
的单调增区间;
(Ⅲ)证明直线![]() 于函数
于函数![]() 的图像不相切
的图像不相切![]()
全国卷Ⅱ(理)
(17)(本小题满分12分)
设函数![]() ,求使
,求使![]() 的
的![]() 取值范围.
取值范围.
全国卷Ⅲ(理)
17.(本小题满分12分)
甲.乙.丙三台机器是否需要照顾相互之间没有影响![]() 已知在某一个小时内,甲.乙
已知在某一个小时内,甲.乙
都需要照顾的概率是0.05,甲.丙都需要照顾的概率是0.05,乙.丙都需要照顾的
概率是0.125![]()
1)求甲.乙.丙三台机器在这一个小时内各自需要照顾的概率?
2)计算在这一个小时内至少有一台需要照顾的概率?
北京卷(理)
15 (本小题共13分)
已知函数![]()
![]()
(I)求![]() 的单调递减区间;
的单调递减区间;
(Ⅱ)若![]() 在区间[一2,2]上的最大值为20,求它在该区间上的最小值
在区间[一2,2]上的最大值为20,求它在该区间上的最小值![]()
天津卷(理)
(17)(本小题满分12分)
在![]() 中,
中,![]() 所对的边长分别为
所对的边长分别为![]() ,设
,设![]() 满足条件
满足条件
![]() 和
和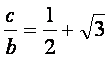 ,求
,求![]() 和
和![]() 的值
的值
上海卷(理)
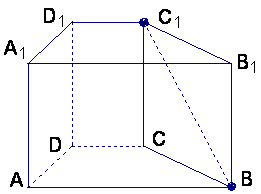
17.已知直四棱柱![]() 中,
中,![]() ,底面
,底面![]() 是直角梯形,
是直角梯形,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,求异面直线
,求异面直线![]() 与
与![]()
所成的角的大小![]() (结果用反三角函数表示)
(结果用反三角函数表示)
辽宁卷
17.(本小题满分12分)
已知三棱锥P—ABC中,E、F分别是AC、AB的中点,△ABC,△PEF都是正三角形,PF⊥AB.
(Ⅰ)证明PC⊥平面PAB;
(Ⅱ)求二面角P—AB—C的平面角的余弦值;
(Ⅲ)若点P、A、B、C在一个表面积为12π的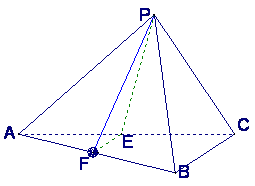
球面上,求△ABC的边长.
江苏卷
19.(本小题满分12分)如图,圆![]() 与圆
与圆![]() 的半径都是1,
的半径都是1,![]() ,
,
过动点P分别作圆![]() .圆
.圆![]() 的切线PM、PN(M.N分别为切点),使得
的切线PM、PN(M.N分别为切点),使得![]()
![]()
试建立适当的坐标系,并求动点P的轨迹方程![]()
浙江卷(理)
15.已知函数f(x)=-![]() sin2x+sinxcosx.
sin2x+sinxcosx.
(Ⅰ)
求f(![]() )的值;
)的值;
(Ⅱ)
设![]() ∈(0,
∈(0,![]() ),f(
),f(![]() )=
)=![]() -
-![]() ,求sin
,求sin![]() 的值.
的值.
福建卷(理)
17.(本小题满分12分)
已知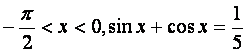 .
.
(I)求sinx-cosx的值;
(Ⅱ)求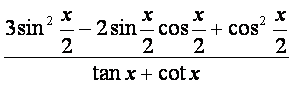 的值.
的值.
湖北卷(理)
17.(本小题满分12分)
已知向量a=(![]() ,x+1),b=
(1-x,t)
,x+1),b=
(1-x,t)![]() 若函数
若函数![]() =a·b在区间(-1,1)上
=a·b在区间(-1,1)上
是增函数,求t的取值范围![]()
湖南卷(理)
16.(本小题满分12分)
已知在△ABC中,sinA(sinB+cosB)-sinC=0,sinB+cos2C=0,
求角A、B、C的大小.
广东卷
15.(本小题满分12分)
化简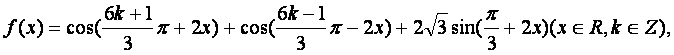
并求函数![]() 的值域和最小正周期.
的值域和最小正周期.
重庆卷(理)
17.(本小题满分13分)
若函数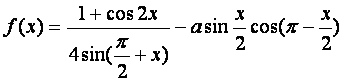 的最大值为2,试确定常数a的值.
的最大值为2,试确定常数a的值.
山东卷(理)
(17)(本小题满分12分)
已知向量![]() 和
和![]() ,
,
且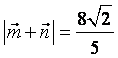 ,求
,求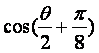 的值
的值![]()
江西卷(理)
17.(本小题满分12分)
已知函数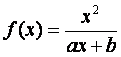 (a,b为常数)且方程f(x)-x+12=0有两个实根
(a,b为常数)且方程f(x)-x+12=0有两个实根
为x1=3, x2=4.
(1)求函数f(x)的解析式;
(2)设k>1,解关于x的不等式;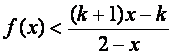
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。