解答题

17、(本题满分12分)

    已知复数z₁满足(1+i)z­₁=－1+5i, z­₂=a－2－i, 其中i为虚数单位,

a∈R, 若<,求a的取值范围.

  解答

18、(本题满分12分)

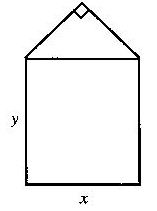  某单位用木料制作如图所示的框架, 框架的下部是边长分别为

  x、y(单位：m)的矩形.上部是等腰直角三角形. 要求框架围成的总面积8cm².

  问x、y分别为多少(精确到0.001m) 时用料最省?

     解答

19、(本题满分14分) 第1小题满分6分, 第2小题满分8分

  记函数f(x)=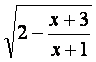的定义域为A, g(x)=lg[(x－a－1)(2a－x)](a<1)

 的定义域为B.

(1) 求A；

(2) 若BA, 求实数a的取值范围.

 解答

20、(本题满分14分) 第1小题满分6分, 第2小题满分8分

  已知二次函数y=f₁(x)的图象以原点为顶点且过点(1,1),反比例函数

y=f₂(x)的图象与直线y=x的两个交点间距离为8,f(x)= f₁(x)+ f₂(x).

 (1) 求函数f(x)的表达式；

 (2) 证明:当a>3时,关于x的方程f(x)= f(a)有三个实数解.

 解答

21、(本题满分16分) 第1小题满分4分, 第2小题满分6分, 第3小题满分6分

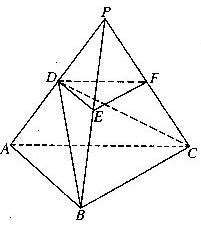  如图,P-ABC是底面边长为1的正三棱锥,D、E、F分别为棱长PA、PB、PC上

的点, 截面DEF∥底面ABC, 且棱台DEF-ABC与棱锥P-ABC的棱长和相等.

(棱长和是指多面体中所有棱的长度之和)

(1)     证明：P-ABC为正四面体；

(2)     若PD=PA, 求二面角D-BC-A的

大小；(结果用反三角函数值表示)

(3)     设棱台DEF-ABC的体积为V, 是

否存在体积为V且各棱长均相等的直

平行六面体,使得它与棱台DEF-ABC

有相同的棱长和? 若存在,请具体构造

出这样的一个直平行六面体,并给出证

明；若不存在,请说明理由.

  解答

22、(本题满分18分) 第1小题满分6分, 第2小题满分4分, 第3小题满分8分

  设P₁(x₁,y₁), P₁(x₂,y₂),…, P_n(x_n,y_n)(n≥3,n∈N) 是二次曲线C上

的点, 且a₁=², a₂=², …, a_n=²构成了一个公差为d(d≠0) 的

等差数列, 其中O是坐标原点. 记S_n=a₁+a₂+…+a_n.

(1)      若C的方程为=1,n=3. 点P₁(3,0) 及S₃=255, 求点P₃的坐标；

 (只需写出一个)

(2)若C的方程为(a>b>0). 点P₁(a,0), 对于给定的自然数n, 当公

差d变化时, 求S_n的最小值；

. (3)请选定一条除椭圆外的二次曲线C及C上的一点P₁,对于给定的自然数n,

写出符合条件的点P₁, P₂,…P_n存在的充要条件,并说明理由.

 解答