解答题

（17）（本小题满分12分）

已知6sin²α+sinαcosα－2cos²α=0，，求的值。

 解答

（18）（本小题满分12分）

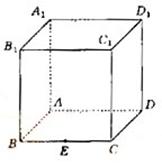如图，在棱长为1的正方体ABCD－A₁、B₁、C₁、D₁中，点E是棱BC的中点，

点F 是棱CD上的动点。

（Ⅰ）试确定点F的位置，使得D₁E⊥平面AB₁F；

（Ⅱ）当D₁E⊥平面AB₁F时，求二面角C₁―EF―A的大小

（结果用反三角函数值表示）。

                          解答

（19）（本小题满分12分）

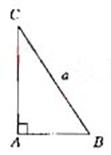如图，在Rt△ABC中，已知BC=a,若长为2 a的线段P  Q以点A为中点，

问与的夹角θ取何值时，的值最大？并求出这个最大值。

 　　　　　　　　　　　　　　解答

（20）（本小题满分12分）

直线：与双曲线C：的右支交于不同的两点A、B。

（Ⅰ）求实数的取值范围；

（Ⅱ）是否存在实数，使得以线段AB为直径的圆经过双曲线C的右焦点F？

若存在，求出的值。若不存在，说明理由。

　解答

（21）（本小题满分12分）

某突发事件，在不采取任何预防措施的情况下发生的概率为0.3；一旦发生，

将造成400万元的损失。现有甲、乙两种相互独立的预防措施可供采用。

单独采用甲、乙预防措施所需的费用分别为45万元和30万元，采用相应预防

措施后此突发事件不发生的概率分别是0.9和0.85。若预防方案允许甲、乙

两种预防措施单独采用、联合采用或不采用，请确定预防方案使总费用最少。

（总费用=采取预防措施的费用+发生突发事件损失的期望值。）

　解答

（22）（本小题满分14分）

已知，数列满足n=1，2，…。

（Ⅰ）已知数列极限存在且大于零，求A=(将A用表示)；

（Ⅱ）设…，证明：；

（Ⅲ）若对…，都成立，求的取值范围。

 　解答