解答题
全国卷Ⅰ(文)
18.(本小题满分12分)
求函数![]() 的最小正周期、最大值和最小值.
的最小正周期、最大值和最小值.
全国卷Ⅱ(文)
18.(本小题满分12分)
已知锐角三角形ABC中,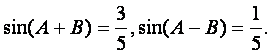
(Ⅰ)求证![]() ;
;
(Ⅱ)设AB=3,求AB边上的高.
全国卷Ⅲ(文)
18.(本小题满分12分)已知![]() 为锐角,且
为锐角,且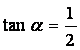 ,求
,求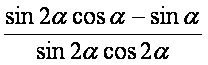 的值.
的值.
全国卷Ⅳ(文)
18.(本小题满分12分)
已知数列{![]() }为等比数列,
}为等比数列,![]()
(Ⅰ)求数列{![]() }的通项公式;
}的通项公式;
(Ⅱ)设![]() 是数列{
是数列{![]() }的前
}的前![]() 项和,证明
项和,证明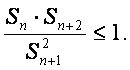
天津卷(文)
18.(本小题满分12分)
从4名男生和2名女生中任选3人参加演讲比赛。
(1)求所选3人都是男生的概率;
(2)求所选3人中恰有1名女生的概率;
(3)求所选3人中至少有1名女生的概率。
辽宁卷
18.(本小题满分12分)
设全集U=R
(1)解关于x的不等式![]()
![]()
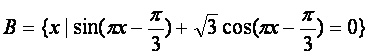 ,
,
若( ∪A)∩B恰有3个元素,求a的取值范围.
江苏卷
18.在棱长为4的正方体ABCD-A1B1C1D1中,O是正方形A1B1C1D1的中心,
点P在棱CC1上,且CC1=4CP.
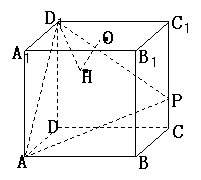 (Ⅰ)求直线AP与平面BCC1B1所成的角的大小(结果用反三角函数值表示);
(Ⅰ)求直线AP与平面BCC1B1所成的角的大小(结果用反三角函数值表示);
(Ⅱ)设O点在平面D1AP上的射影是H,求证:D1H⊥AP;
(Ⅲ)求点P到平面ABD1的距离.
浙江卷(文)
(18)(本题满分12分)
在ΔABC中,角A、B、C所对的边分别为a、b、c,且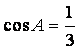 。
。
(Ⅰ)求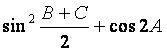 的值;
的值;
(Ⅱ)若![]() ,求bc的最大值。
,求bc的最大值。
福建卷(文)
18.(本小题满分12分)
甲、乙两人参加一次英语口语考试,已知在备选的10道试题中,甲
能答对其中的6题,乙能答对其中的8题.规定每次考试都从备选题中
随机抽出3题进行测试,至少答对2题才算合格.
(Ⅰ)分别求甲、乙两人考试合格的概率;
(Ⅱ)求甲、乙两人至少有一人考试合格的概率.
湖北卷(文)
18.(本小题满分12分)
如图,在棱长为1的正方体ABCD—A1B1C1D1中,AC与BD交于点E,
CB与CB1交于点F.
(I)求证:A1C⊥平BDC1;
(II)求二面角B—EF—C的大小(结果用反三角函数值表示).
湖南卷(文)
18.(本小题满分12分)
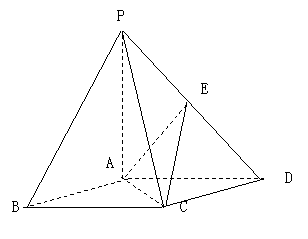
如图,在底面 是菱形的四棱锥P—ABCD中,∠ABC=600,PA=AC=a,
PB=PD=![]() ,点E是PD的中点.
,点E是PD的中点.
(I)证明PA⊥平面ABCD,PB∥平面EAC;
(II)求以AC为棱,EAC与DAC为面的二面角![]() 的正切值.
的正切值.
重庆卷(文)
18.(本小题满分12分)
设甲、已、丙三人每次射击命中目标的概率分别为0.7、0.6和0.5。
(1) 三人各向目标射击一次,求至少有一人命中目标的概率及恰有
两人命中目标的概率;
(2) 若甲单独向目标射击三次,求他恰好命中两次的概率。
北京卷(文)
(16)(本小题满分14分)
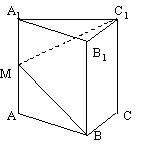
如图,在正三棱柱![]() 中,AB=2,
中,AB=2,![]() ,由顶点B沿棱柱侧
,由顶点B沿棱柱侧
面经过棱![]() 到顶点
到顶点![]() 的最短路线
与
的最短路线
与![]() 的交点记为M,求:
的交点记为M,求:
(I)三棱柱的侧面展开图的对角线长
(II)该最短路线的长及![]() 的值
的值
(III)平面![]() 与平面ABC所成二面角(锐角)的大小
与平面ABC所成二面角(锐角)的大小
上海卷(文)
18、(本题满分12分)
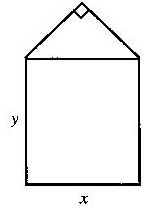 某单位用木料制作如图所示的框架,
框架的下部是边长分别为
某单位用木料制作如图所示的框架,
框架的下部是边长分别为
x、y(单位:m)的矩形.上部是等腰直角三角形. 要求框架围成的总面积8cm2.
问x、y分别为多少(精确到0.001m) 时用料最省?
广东卷
18. (12分)如右下图,在长方体ABCD—A1B1C1D1中,已知AB= 4, AD =3, AA1= 2.
E、F分别是线段AB、BC上的点,且EB= FB=1.
(1)
求二面角C—DE—C1的正切值;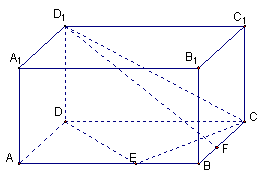
(2) 求直线EC1与FD1所成的余弦值.
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。