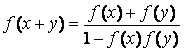 .
.一、选择题(每小题5分)
6.给出下列三个等式:![]() ,
,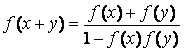 .
.
下列函数中不满足其中任何一个等式的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.某班50名学生在一次百米测试中,成绩全部介
于13秒与19秒之间,将测试结果按如下方式分成六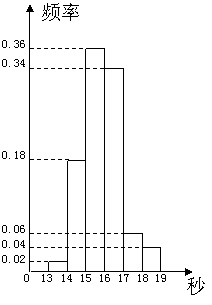
组:每一组,成绩大于等于13秒且小于14秒;第二
组,成绩大于等于14秒且小于15秒;……第六组,
成绩大于等于18秒且小于等于19秒.右图是按上述
分组方法得到的频率分布直方图,设成绩小于17秒
的学生人数占全班人数的百分比为![]() ,成绩大于等于
,成绩大于等于
15秒且小于17秒的学生人数为![]() ,则从频率分布直方
,则从频率分布直方
图中可以分析出![]() 和
和![]() 分别为(
)
分别为(
)
A.![]() B.
B.![]()
C.![]() D.
D.![]()
11.设函数![]() 与
与 的图象的交点为
的图象的交点为![]() ,
,
则![]() 所在的区间是(
)
所在的区间是(
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题(每小题4分)
13.设函数![]()
![]() ,则
,则![]() .
.
14.函数![]() 的图象恒过定点
的图象恒过定点![]() ,若点
,若点![]() 在直线
在直线![]() 上,
上,
则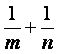 的最小值为
.
的最小值为
.
三、解答题
19.(本小题满分12分)
本公司计划2008年在甲、乙两个电视台做总时间不超过300分钟的广告,广告总费用
不超过9万元,甲、乙电视台的广告收费标准分别为![]() 元/分钟和200元/分钟,规定
元/分钟和200元/分钟,规定
甲、乙两个电视台为该公司所做的每分钟广告,能给公司事来的收益分别为0.3万元
和0.2万元.问该公司如何分配在甲、乙两个电视台的广告时间,才能使公司的收益
最大,最大收益是多少万元?
21.(本小题满分12分)
设函数![]() ,其中
,其中![]() .
.
证明:当![]() 时,函数
时,函数![]() 没有极值点;当
没有极值点;当![]() 时,函数
时,函数![]() 有且只有
有且只有
一个极值点,并求出极值.
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。